Closed Loop control systems can handle a wide range of motions with a wide range of loads if the control system and mechanics are properly designed for the task. A couple of the more difficult combinations to design for are high inertial mismatches and backlash with hard gearing. The question is not just how to make the system stable, but rather how to also get the desired performance.

Different approaches are needed for rapid motions with a light load versus those required for high inertia loads, especially in the presence of stiction. Additional requirements may include minimizing acoustical noise and having stability in the presence of backlash. 

Yet another tuning complexity occurs when encountering variable stiffness especially with variable loads, for example, a coupling with a significant varying load to a motor using a belt drive. In this case, the effective distance between the motor and the load—as seen through the portion of the belt under tension—varies as the position varies, and as the direction of applied force varies. The resonance frequency of such a system varies with a) the position, b) belt tension—which varies with the motor torque, and c) the inertia of the load, which may change if the system is being used to transport materials. 

There are also other motion optimizations that are dependent on the application. A precision liquid dispensing application, for example, requires not only that no overshoot occurs, but also requires that the liquid deceleration be kept low enough to avoid cavitation (bubble formation) in the liquid stream. Note that some other liquid dispensing techniques may intentionally shock the flow to dispense drops of liquid through the air without leaving a drop hanging.  Overshoot in either of these cases would affect the dispense volume accuracy in an undesired way. 

Animatronics also tend to come in two flavors: those that try to look lifelike want the final position to slide into place, while those moving like a robot want the motion to snap into place from a fixed speed and often with as high of acceleration as is reasonable to “stick the landing.”

Another confounder for control engineers is stiction. Stiction is the significant increase in friction as the speed goes below a critical threshold; the friction increase can cause the sliding parts to grab and may completely stop the motion until the force is raised enough to again overcome the low speed friction. The resulting breakaway action is then capable of causing a lurching if not properly handled. A common example is a sealed piston pumping liquid. These may have significant breakaway force and may also studder in the delivery stroke if the servo is not properly tuned to overcome the stiction. Animatronics does not look smooth if the stiction is not properly handled, and machining operation will not be smooth if stiction causes the motion to be jerky.

This material will be covered in a multipart article that goes through these related but different issues. We will first dive into the underlying issues and then how to address them via the control system. I will try to minimize the math and stick to the heuristics to keep this from requiring a master’s or higher in controls systems to follow! I’m also going to focus on rotary motors as they are most common, but the same techniques apply to linear motors.

High Inertia Mismatch Problem

High inertia mismatch describes when the effective inertia of the load (as seen by the motor) is significantly higher than the motor inertia. This is particularly problematic if there is significant compliance (i.e., a springy coupling or backlash) between the motor and the load. 

In many cases, the problem can be simplified by use of tooth belts and pulleys or gear heads to gear down the motor to the load. For a gear ratio of N:1, the effective inertia is reduced by a factor of N². The load acceleration is N times lower than motor acceleration, and the force/torque to the load is N times greater than the force/torque seen at the motor. The resulting effect is that a 10:1 gear can reduce the reflected inertia by a factor of 100. However, this introduces additional parts into the system that can wear and typically need maintenance, as well as the size and weight effects. 

Most PID systems require an inertial mismatch to be below about 8.7:1 for stability, which can require either multiple reduction stages or adjustments to the control system, or other techniques.

Most servo systems measure the position of the motor shaft (and often the back shaft of the motor). For light loads with stiff coupling, the load can appear to just be an extension of the motor inertia, with any resonance frequencies above the bandwidth of the servo.  Placing the feedback before any reduction gearing/pulleys gives a higher effective resolution to the measurement, so for simple/light load systems, this works well. 

Gears, however, have cost, size, weight, and maintenance impacts. If the gears are not tight or have worn, they may also cause backlash/play in the system. When a servomotor reverses direction, the load decouples from the motor until the motor has moved far enough to have the opposite side of the teeth engage and couple to the load again. On impact, the teeth can bounce sufficiently to cause the system to go into a limit cycle where it buzzes with rapid motion reversals. This oscillation happens due to the system gain (angular acceleration divided by current) greatly increases while the teeth are not coupling the load inertia to the motor. The materials of the teeth can significantly affect the rebound energy when the teeth hit, so careful selection can help mitigate this issue.

When direct drive coupling is used, the system can be very responsive, but more care is needed to keep the system stable. As the inertial mismatch increases, the shaft/couplers between the motor and the load form a spring. Spiral couplers can have real difficulty in servo system due to their lower stiffness.

At low frequencies, the shaft may seem quite stiff, and the inertia seen by the motor is just the motor inertia plus the load inertia: Jt = Jm + Jl (My electrical background uses the letter I for other purposes, but mechanical types may call inertia I!)  This just ignores the effects of the shaft.

As the frequency increases, the spring effect of the shaft does not allow the load inertia to accelerate as quickly as the motor which is attached. The shaft starts to twist so that the angle of the load is no longer the same as the angle of the motor. The minimum response will come at an antiresonance frequency where the two masses are moving in opposite directions. The gain of the system then increases with frequency as the main contribution to the load seen by the motor is the torsion of the shaft. This continues up to a resonance at the peak of the curve, after which the inertia of the motor then dominates the load seen by the motor. 

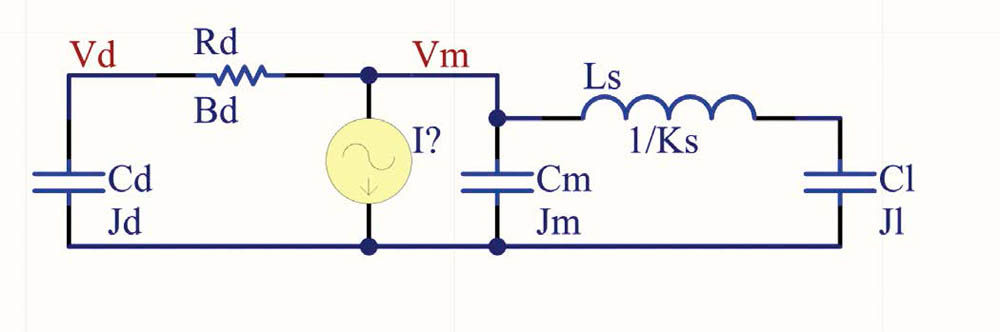
Note that his model is simplified, having no damping, whereas real systems have some losses due to material heating when flexing occurs. Adding damping reduces the resonant and antiresonance peaks, but a fairly low loss system will look similar. The electronic model will be a low pass Pi filter, where the torque is modeled as a current, the motor and load inertias are modeled as capacitors, and the spring of the shaft is modeled as an inductor. The value of the inductor is 1/k as a zero-value inductor would represent an infinite stiffness shaft. The motor velocity is Vm, while the load velocity is Vl which would be modeled as voltages in the electronic style model.

We calculate the gain in dB = 20 * log₁₀ (gain), where we are looking at the output velocity versus torque. The frequency scale is plotted on a log₁₀ basis. This allows us to easily look at the gains over a wide range of frequencies.

(These can all be readily modeled in Excel using complex math functions. See sidebar.)

Chart 1 shows the gain for a 1:1 inertial mismatch. The downward peak is the antiresonance. The upward peak is the resonance.

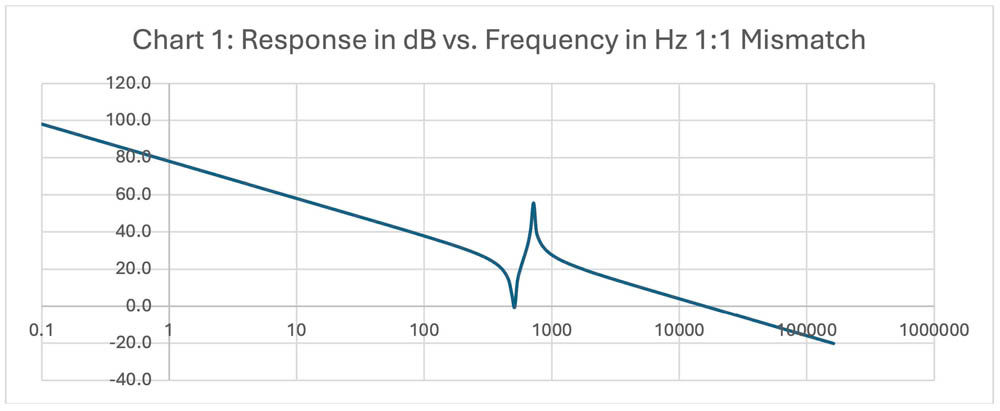
Chart 2 shows the significantly greater gain increase for a 10:1 inertial mismatch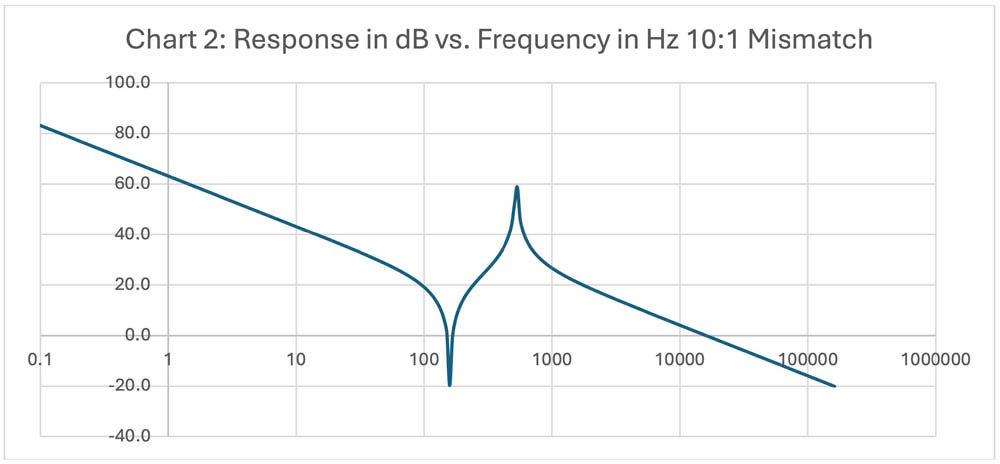

Chart 3 shows the effect for a 100:1 inertia mismatch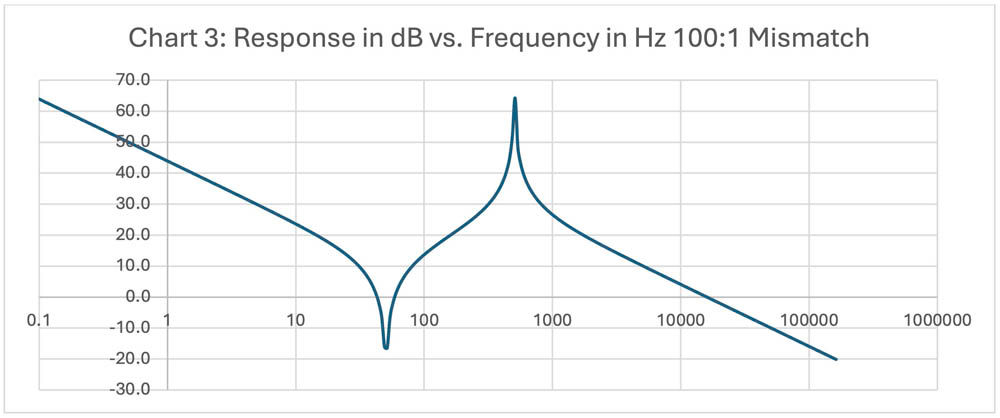

Chart 4 shows the resulting phase angle

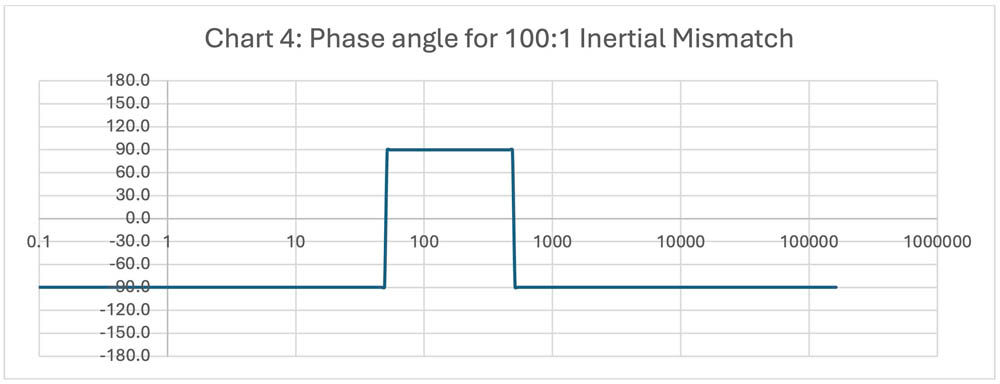
You will see in each case the maximum gain from the resonance and the resonance frequency does not change much with the mismatch, as this is mostly determined by the motor inertia and the spring constant of the shaft and coupler. However, the anti-resonance frequency goes down by the square root of (1+inertial mismatch), that is by the square root of the motor plus load inertia.

The low frequency gain drops as 1/(Jm + Jl) that is as 1/total inertia. This is expected as a very large inertial load will accelerate much more slowly than a light inertial load. The control engineer would normally increase the gain of the system to try to make it more responsive.

The problem comes in the upward slope portion of the curve. As the inertial mismatch increases, the gain between the low frequency line (1/(Jm+Jl) and the high frequency line (1/Jm) gets larger, increasing the chance that the system will go into oscillation.

It is also interesting to note that the phase jumps from -90 when the inertia dominates, to +90 when the spring dominates, and back to -90 when the inertia again dominates. 

There are a couple of methods to help stabilize such a high inertial load. The first is to add a low pass filter to the velocity estimator for the control loop. The extra filtering will increase lag in the velocity estimate but will reduce the gain at higher frequencies. This can be considered as making a better estimate of the actual load velocity which continues to reduce with frequency, unlike the sensor on the motor shaft. We can take advantage of the phase boost (+90 degrees) between the antiresonance and resonance frequencies to counter the lag effect of a 2nd order low pass filter to reduce the gain boost associated with the resonance without losing too much phase margin. We will address this in more detail later in this series of articles.

Another method is to add a viscous inertial damper to the motor. 

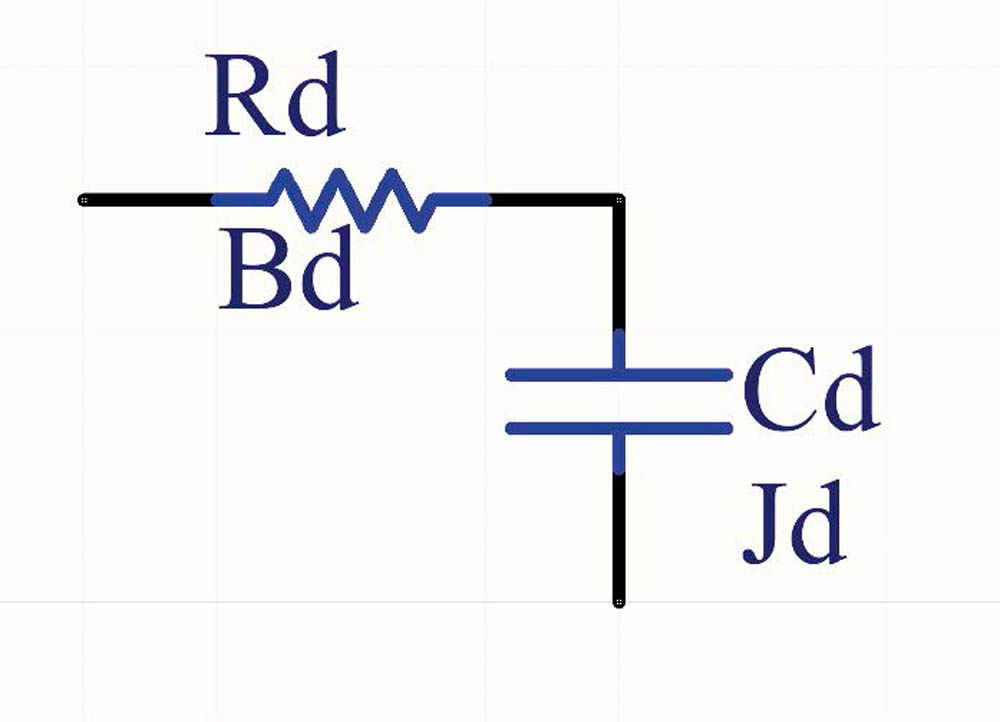
A viscous inertial damper typically has a fairly low inertia housing which contains a higher inertial cylinder which couples to the housing via thick silicone grease. At low accelerations, there is little shear in the grease, and the load looks mostly like a simple inertia. At higher accelerations, the shearing increases, with the inertial damper not significantly moving compared to the input shaft, and the resulting load looking mostly like a like a damper. For a rotary load operating at constant velocity, the inertial load will spin at the same speed as the motor shaft and only a little additional load is introduced. For oscillations in the shaft speed, as the oscillation frequency increases, the shearing of the coupling grease increases, adding damping to the system.

Assuming the housing inertia is low compared to the motor, we can model the shear of the grease as causing a torque to the damper inertia proportional to the difference in radial speed between the case and the damper inertia. 

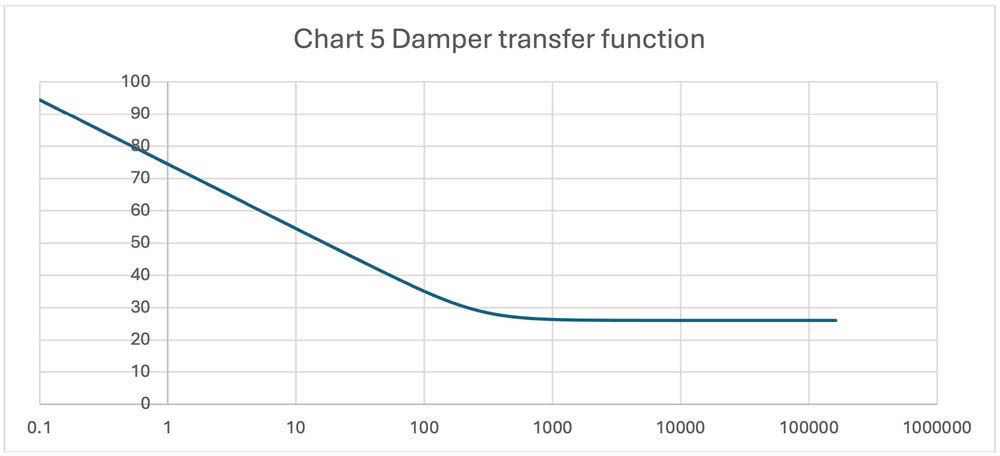
This damper has an inertia about 3x motor inertia, and 1/33 of the load inertia, and the viscous term was adjusted to optimize the shape of the combined curve.

The damper is shown mounted to the motor inertia (stiff compared to the viscous coupling of the grease) with the 100:1 inertia attached to the motor via a shaft

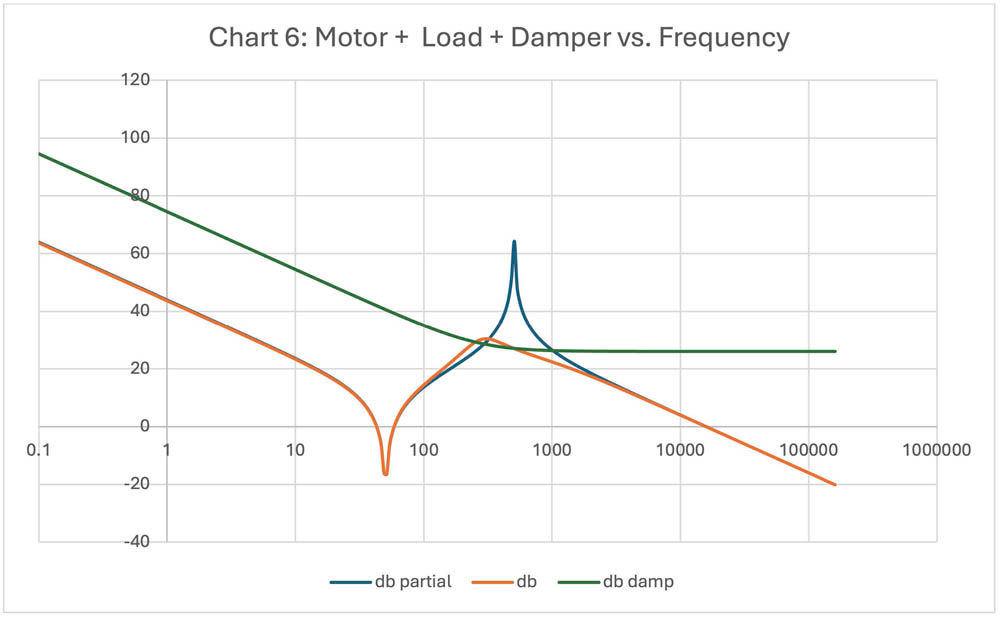
Chart 6 shows the effects when the damper (green) is connected to the motor and 100:1 inertial load (blue) to produce the damped system (orange).

When the damper is placed on the motor shaft, the impedance of the motor with load goes from the dB partial (blue curve) to the dB (orange curve), which has a peak ~ 64 dB down to a peak around 30 dB, almost 64 dB lower. This allows the system gain to be significanlty increased while avoiding oscillations.

This reduced gain spike makes for a system that is much easier to control. Later articles in this series will show how we can produce a similar result electronically in the control system without the need for the mechanical damper.

The charts were all produced in Excel using the complex math function which may be loaded as an extension. This website: https://www.exceldemy.com/learn-excel/math/complex-numbers/ has a nice chart of these functions.

QuickSilverControls.com