Smashing the Efficiency Barrier
Smashing the Efficiency Barrier — A Practical Comparison of Planetary and Orbitless Gear-Heads
Introduction
An Orbitless (patent pending) gear-head is a novel fixed-ratio epicyclic gear-head with crank-shaft planet pinions and two carriers, but no ring gear. It provides half the reduction ratio of a planetary gear-head with similar pinions and shares many characteristics such as torque splitting and co-axial drive shafts that spin in a common direction. Three prototype Orbitless gear-heads are constructed, each with a different planet support mechanism. It is shown that load capacity is marginally improved by using ball instead of plain bearings, and greatly improved by mounting the bearings to the planets rather than the carriers. In comparison to an off-the-shelf planetary gear-head, friction losses are reduced by up to 59% and total input power is reduced by up to 33% over the operating range of the motor and gear-head.
Fixed ratio speed reducers may be broadly classified as high or low-ratio, depending on whether they provide a ratio that is above or below approximately 10:1(Ref. 1). High-ratio designs are numerous and include the worm, cycloid, orbit, nutating, harmonic (Ref. 4), stepped-planet (Ref. 3) and bi-coupled planetary gear-heads. Each is arguably an implementation of one of two fundamental low-ratio gear-head configurations — the offset and planetary — both of which are literally thousands of years old.
In (Refs. 7-8), the Orbitless gear-head is proposed, which is a third low-ratio configuration that shares various advantages with offset and planetary gear-heads. Like an offset gear-head, it may be made entirely from pinions and does not experience reverse bending. Like a planetary gear-head, it has load sharing, sequential meshing, in-line drive axes (optional) and a common drive direction. However, it has a lower pitch line velocity which is shown to improve efficiency, and a lower planet bearing velocity, which extends the computed bearing life.
In this paper, the Orbitless gear-head properties are summarized. Three prototype gear-heads are constructed using off-the-shelf components. Load capacity, speed, and efficiency are measured in a series of destructive tests, and the results are compared to a commercial planetary gear-head. It is shown that the Orbitless prototype has a comparable load capacity and significantly higher efficiency than the planetary gear-head.
Anatomy of an Orbitless Gear-Head
An Orbitless gear-head resembles a planetary gear-head in that a high-speed (input) shaft drives a sun pinion which is surrounded by a collection of planet pinions that ride on an output carrier which drives a low-speed (output) shaft (Fig. 1). Instead of an orbit (ring) gear, an Orbitless gear-head includes a second reaction carrier which engages each planet on a second planet axis. Although the two planet axes must not coincide, they may otherwise reside anywhere. Orbitless planets do not rotate. They circulate the sun at a fixed orientation so neither planet axis must intersect the planet center.

In Figure 1, two versions are shown. The in-line version on the left has its drive carrier planet axes intersecting the center of each planet which results in co-axial input (high-speed) and output (low-speed) shafts. The offset version on the right has symmetrically offset planet axes which accommodates larger planet bearings for longer bearing life but has an offset between the input and output shafts that is equal to the drive carrier planet axis offset. The reduction ratio i, planet bearing velocity ωP, and pitch line velocity plv of a planetary and Orbitless gear-head are derived (Ref. 9) and shown in equations (1–6), where s and p are the numbers of teeth on the sun and planet, ωS is the angular velocity of the sun (high-speed shaft) and M is the tooth module.

Prototype Orbitless Gear-Head Design
A prototype offset Orbitless gear-head is constructed using OTS pinions from a Faulhaber Series 20/1 planetary gear-head with a 27-tooth sun; three 27-tooth planets; a module of M = 0.22; and a ratio of i = 2:1. It has 1mm OD planet journals — each spaced 1.1mm from the planet center — resulting in a 1.1 mm offset between the high-speed (sun) and low-speed (carrier) shafts. Uniform 27-tooth sun and planet pinions do not provide sequential meshing or tooth hunting, but satisfy an availability constraint. The baseline for comparison is a commercial 20/1 planetary gear-head with a 21-tooth sun; three 18-tooth planets; a module of M = 0.22; a ratio of i = 3.71:1; a speed rating of 5,000 rpm; and a stall torque of 500 mNm (Ref. 7).
Planet bearings are typically the most stressed members in an epicyclic gear-head and are often the first to fail. Since Orbitless planets are supported by two bearings, space constraints limit bearing size — which raises durability concerns. To best address this design challenge, the three different Orbitless planet supports (V1-V3) (Figs. 2-3) are constructed, evaluated and compared.


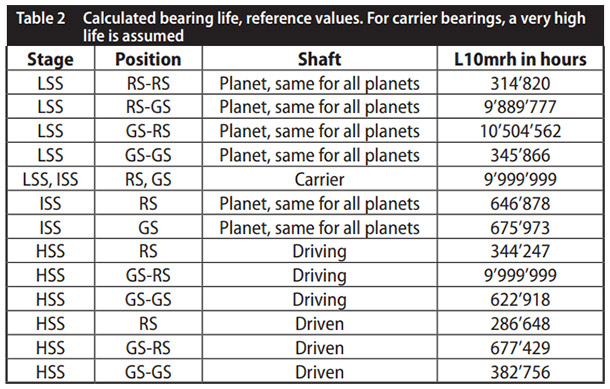
In V1, the journals are interference fit into the planets and the bushings (plain bearings) are interference fit into the carriers. In V2, single-row, deep-groove ball-bearings replace the carrier bushings of V1. In V3, journals are interference fit into the carriers and bushings are interference fit into the planets. The L10 bearing life is calculated using the equations (Ref. 2) for an Orbitless gear-head with an input torque τHS = 17 mNm, s = 27, M = 0.22, pressure angle ϕ = 20°, N = 3. The bearing speed is ωP = 2,500 rpm when ωS = 5,000 rpm (Eq. 5). Using 1×3×1 GRW deep-groove radial ball-bearings with a load rating of C = 82N, L10 = 47,418 hours, or 5.4 years, for the drive carrier and L10 = 64,023 hours, or 7.3 years, for the reaction carrier. This is well in excess of the 1 year rule-of-thumb for acceptable bearing life.
Test Fixture and Destructive Test Sequence
To evaluate load capacity, efficiency and speed rating, each gear-head is mounted to a Faulhaber 24V, 68W Series 2057-S-024-B 2-pole brushless DC-servomotor. The motor has a maximum speed of 55,000 rpm, a stall torque of 155 mNm and a maximum recommended continuous torque of 17 mNm at 5,000 rpm (Ref. 5). The motor is driven by a Faulhaber SC-2804 PWM speed controller (Ref. 6) and is controlled using Faulhaber Motion Manager 6 software. The gear-motor is mounted in an aluminum fixture and is connected to a Magtrol HB-32-3 electromagnetic hysteresis brake using an Oldham coupling. The speed controller and brake are each powered by a GoldStar GP4303A power supply. The same lubrication is used in all gear-heads, and all tools and test equipment have up-to-date calibration. The test fixture is shown (Fig. 4).

The applied load torque τLS is set such that the applied motor torque τHS consistent. It is computed based on an estimated 88% planetary gear-head efficiency and 95% Orbitless gear-head efficiency. The hysteresis brake current is adjusted until the desired output torque is recorded using a Honeywell model 651C-1 and 651C-2 torque watch. Due to its higher estimated efficiency, the Orbitless gear-head delivers approximately 8% more output power to the load during each test phase.
The test parameters are specified (Table 1) where ωHS, ωLS, τHS and τLS are the angular velocity and torque of the high-speed input and low-speed output shafts respectively, and POUT is the power dissipated by the load. Each phase is run for 24 hours and the test is concluded once any abnormal behavior is detected, such as a change in sound or a substantial increase in current draw. The gear-heads are inspected periodically between phases to identify the onset of lubricant or mechanical failure. Phase 1 is a break-in period at no-load, Phase 2 is at the rated speed of the 20/1 gear-head, and Phase 3 is at 2× the rated speed. In phases 2 and 3, the load is increased incrementally until the motor torque reaches its maximum- rated continuous torque (17 mNm uncooled) (Ref. 5) and in phase 4 the speed is increased incrementally while the motor torque is held at 17 mNm.
Gear-Head Failure Modes and Probable Causes
The destructive test sequence described in Table 1 is conducted for the 20/1 planetary gear-head and each Orbitless gear-head version. Upon failure, each gear-head is disassembled, inspected, and the symptoms are documented. The onset of failure is detected with the planetary gear-head during Phase 4a at 12,000 rpm, which is expected after applying a reasonable safety margin to its 5,000 rpm manufacturer-specified speed rating. In Table 2, the test phase when failure occurred, the failure mode and the post- failure observations are tabulated for all gear-heads.
A post-failure inspection of the Version 1 Orbitless gear-head shows wear patterns on the journals where they align with the lateral faces of the bushings. The clockwise tooth face of the V1 sun gear is also visibly worn. Wear patterns on the carrier faces suggest that the planets contacted the carriers as a result of the conical bushing wear that was also observed. A post-failure inspection of the Version 2 Orbitless gear-head shows spalling and separation of the carrier mounted ball bearings.
The pre-mature bearing failures of Versions 1 and 2 are attributed to the planet bearings being mounted to the carriers. Since the applied bearing forces are lateral to tooth force, a yaw torque develops on the planets which causes bushing, tooth and lubricant wear in V1, and outright bearing failure in V2. This is illustrated (Fig. 5) where the upper planet axis engages the drive carrier and the lower planet axis engages the reaction carrier.

The ball-bearings are more robust to yaw torque and increase the load capacity of V2 over V1 by approximately 40%. Mounting the bushings in the planets in V3 vertically aligns all forces, eliminates planet yaw torque, and increases load capacity to a level comparable with the planetary gear-head. It is proposed that load capacity may be further increased by mounting ball-bearings in the planets although space constraints may require a higher reduction ratio since that would introduce larger planet pinions.
The failure mode of the V3 Orbitless gear-head parallels that of the planetary gear-head. In both cases the test was stopped due to a change in sound quality, but no post-failure physical damage or wear was identified other than the initial signs of lubricant separation. In both cases the gear-head remains operational.
Efficiency Measurements
Efficiency values are derived by intermittently recording the current drawn by the motor IM during each 24 hours test cycle and computing the average. The total power input to the system PIN is separated into electrical losses PELEC, mechanical losses PMECH, and power delivered to the load POUT, as shown (Eq. 7). Electrical power losses are separated into impedance losses associated with the controller PC and motor windings PW,and mechanical power losses are separated into friction losses associated with the motor PM and gear-head PG, as shown (Eq. 8).

Load power POUT is taken from Table 1. Motor friction losses PM are computed (Eq. 9) where CM is the manufacturer-specified (Ref. 5) motor friction constant in (mNm/rpm), and gear-head losses PG are computed (Eq. 10) by subtracting the motor friction losses PM and load power POUT from the total mechanical power produced by the motor windings.
In Equation 10, KM is the manufacturer-specified (Ref. 5) motor torque constant in (mNm/A), IM is the measured motor winding current, ωHS is the motor speed, and the product KMIMωHS is the total mechanical power produced by the motor windings.

Motor winding losses PW are computed (Eq. 11) where RM is the manufacturer-specified (Ref. 5) winding resistance in (Ω). Controller losses PC are computed (Eq. 12) where PW + PMECH + POUT is the total power delivered by the controller and ηC is the manufacturer-specified (Ref. 6) controller efficiency in (%).


Equations 7–12 are used to derive gear-head efficiency ηG (Eq. 13) and total system efficiency ηSYS (Eq. 14).


Examples of raw current measurements for Phases 2c and 3f for the planetary 20/1 and Orbitless V3 gear-heads are shown (Fig. 6). The mean value over the entire 24 hour period is also computed and shown for each successfully completed phase.

For each mean current, the individual power components are computed from equations (7–12), and gear-head and total system efficiency are computed from Equations 13–14 and plotted (Figs. 7 and 8).


The largest recorded improvement occurs at 5 W and 5,000 rpm where the planetary 20/1 gear-head demonstrates efficiencies of ηG = 71% (gear-head) and ηS = 46% (system), and the Orbitless V3 gear-head demonstrates efficiencies of ηG = 95% (gear-head) and ηS = 66% (system). This corresponds to relative improvements of 24% and 20%, respectively.
The power losses of all three Orbitless versions are superimposed (Fig. 9). The strong correlation suggests that the measured losses are intrinsic to the gear-head design and are largely independent of planet bearings. Losses do not deviate significantly when ball or sintered bearings are used, or when bearings become worn and approach failure. This further supports the claim that bearing friction does not significantly impact efficiency.

In Figure 9, the gear-head and total system efficiency of the planetary 20/1 and Orbitless V3 gear-heads are also plotted against input speed ωHS, at the maximum-delivered output power POUT, which corresponds to an approximate motor torque of 17 mNm in all cases. Both the gear-head and system efficiency are substantially higher at all speeds with an Orbitless gear-head, and the associated efficiency gain increases with input speed. The reduced pitch and bearing velocities are likely responsible for these apparently superior high-speed characteristics.
Conclusion
Mounting the planet bearings to the carriers induces a planet yaw torque that reduces the load capacity of an Orbitless gear-head. Mounting them to the planets avoids this yaw torque and results in an input load capacity that rivals a planetary gear-head while delivering approximately 8% more output power due to superior efficiency. Although planet bearing size is constrained by planets which must accommodate two non-coaxial bearings, a low rotation rate extends bearing life which is computed to be in excess of 5 years for the example gear-head described here.
An experimental comparison between a prototype Orbitless gear-head and an off-the-shelf planetary gear-head demonstrates dramatic improvements in power consumption due to reduced pitch velocity and fewer gear meshes. When operated at full torque with a load that ranges from 8-20W, the following loss reductions are recorded.
- Gear-head losses: 43%–59%
- Motor winding losses: 24%–45%
- Total system losses: 33%–46%
In addition, total input power, including power delivered to the load, is reduced by up to 33%. For a battery operated system, this means an increase in run time of up to 49%. 
References
- Jelaska, D. Gears and Gear Drives, Wiley, 2012.
- Lynwander, P. “Gear Drive Systems Design and Application,” Marcel Dekker Inc., 1983.
- Muller, H.W. Epicyclic Drive Trains, Wayne State Univ. Press, 1982.
- Musser, C.W. “Strain Wave Gearing,” U.S. Patent #2,906,143, 1959.
- www.micromo.com/products/brushless-dc-motors/brushless-dc-servomotors.
- www.micromo.com/products/drive-electronics/drive-electronics-datasheets.
- www.micromo.com/products/precision-gearheads/precision-gearheads-datasheets.
- Stocco, L.J. Orbitless Gearbox, Patent Cooperation Treaty, CT/CA2015/050423, 2014.
- Stocco, L. Orbitless Drive, ASME International Mechanical Engineering Congress & Exposition, Nov. 2016.
 Leo Stocco is the CTO of Oribitless Drives and the inventor of the Orbitless drive technology. He is a professor in Electrical Engineering at the University of British Columbia where he specializes in electro-mechanical design and medical instrumentation. He obtained his Ph.D. from UBC in the field of mechanical robot optimization and spent five years as the director of robotics at Integrated Surgical Systems in Davis California.
Leo Stocco is the CTO of Oribitless Drives and the inventor of the Orbitless drive technology. He is a professor in Electrical Engineering at the University of British Columbia where he specializes in electro-mechanical design and medical instrumentation. He obtained his Ph.D. from UBC in the field of mechanical robot optimization and spent five years as the director of robotics at Integrated Surgical Systems in Davis California. Robert Gloeckner is R&D Engineer, Advanced Engineering, MicroMo Electronics, Inc.
Robert Gloeckner is R&D Engineer, Advanced Engineering, MicroMo Electronics, Inc.This paper was first presented at the International VDI Conference on Gears 2017, Garching/Munich [VDI-Berichte 2294, 2017, VDI Verlag GmbH] and is reprinted here with VDI approval.