Unlike HVAC applications, servomotors are not normally operated at the same speed or torque for extended periods, thus the overall efficiency of a servomotor is not easily given a single numeric value. The efficiency varies greatly with the application, and thus different applications favor different types of servomotors.

Standards for Conventional Use Synchronous Motors.

Standard motor efficiency classes—IE1 though IE5—are taken using very specific conditions to allow the motors to be quantitively compared. The motors under these classes are compared using direct AC line operation between 50 and 1,000 V, from 1 or 3 phase mains, are limited to 2, 4, 6, or 8 pole motors, and with a power rating of 120 W to 100 kW. The motors are tested at their continuous rated power (at which they may operate without exceeding specified insulation class). Their efficiency varies with line frequency, and so there are different efficiencies for 50 Hz versus 60 Hz operation. The very specific operating conditions reduce ambiguity, which allows for more accurate comparisons between manufacturers.

So how do we compare servomotors?

Efficiency is defined as:

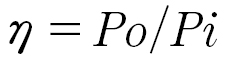
We will use power in watts for both input and output power.

Output power is the mechanical output power at the shaft:

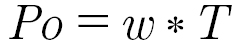
where radial frequency w is measured in radians per second and torque T is measured in Newton-meters.

Electrical input power is measured as watts.

As servomotors use driver electronics, they do not normally operate directly from the line voltage. Further, the voltage and current waveforms driving the motor windings may be complex, thus it is often easier to measure the combined driver and motor efficiencies. This allows the input power to be measured where waveforms are simple, requiring less sophisticated equipment for accurate measurement, and such measurements additionally include the losses of the drive which are important for the total system efficiency. If there is a DC bus input, this is simply: Pi = Vi ∗ Ii ; For AC input, the input power needs to include power factor, including harmonic distortions in the input current. Measuring a particular motor and driver as a set also helps restore some repeatability to the measurements, as the efficiency of the motor will vary with the drive due to harmonic content, chopping style and frequency, commutation method, internal bus voltage, and any output filtering within the drive.

Direct Permanent Magnet versus Indirect Permanent Magnet Motors

Synchronous motors, used to implement both continuous speed motors and brushless servomotors, have several divisions. One dividing category breaks the motors into direct permanent magnet motors, which have the magnets directly facing the rotor-stator air gap, and indirect permanent magnet motors, which have soft magnet materials between the magnet and the air gap. Direct permanent magnet synchronous motors are not normally (not easily) able to have their fields weakened, while the extra soft magnetic material in the indirect permanent magnet motor allows this weakening to be done much more easily.

Direct Permanent Magnet Motor Modeling

The direct permanent magnet motors (also known as surface permanent magnet or SPM) normally do not support field weakening, and produce a fairly flat torque constant over speed, with only a slight droop at higher speeds as losses commonly increase with speed. The current required for a given torque is the torque divided by the torque constant:

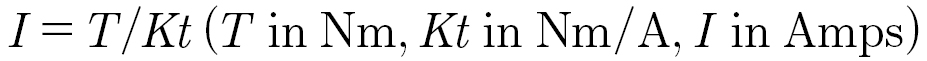
A first order approximation of the drive voltage includes both the back-EMF of the motor and the resistive losses:

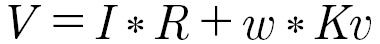
With w in radians per second,and Kv in volts per radian per second then the numeric value of Kv and Kt will be essentially the same (with Kt slightly lowered to lump in other losses; if the losses are accounted for separately, then Kt and Kv should be equal).

For a given torque and velocity:

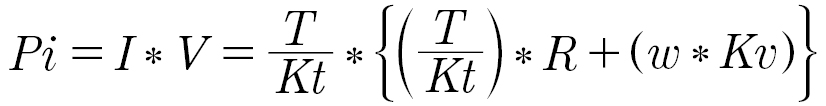
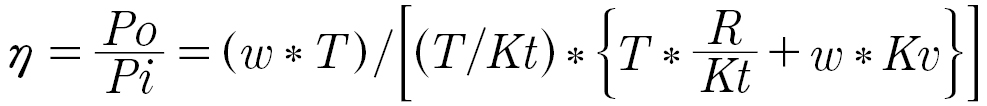
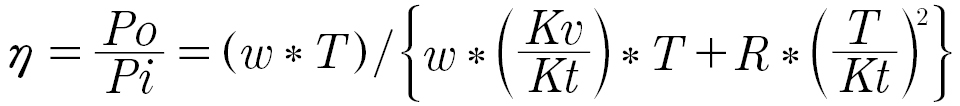
We can bring in another motor factor called “Motor Quality.” When the motor is stationary, the power dissipated in the winding resistance to generate the stationary torque may be calculated:

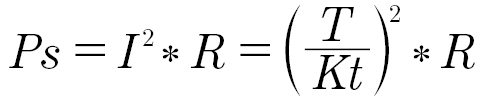
If we define motor quality as: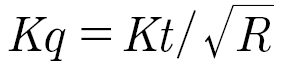

Then the resistive dissipation for a given torque is: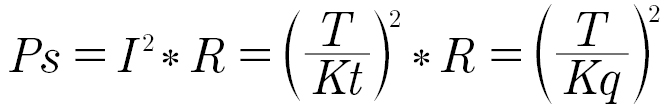

Motor quality Kq is a useful motor parameter when comparing motors as it stays constant over different voltage and current ratings for the same motor mechanical design. That is fewer turns of a heavier wire at the same current density gives the same motor quality. The quality factor goes up with the number of poles, with the gap magnetic field strength, and with the radius of the motor, and goes down with the portion of the stator wiring that is not producing motor torque—the end windings, as this increases the resistance but not the torque constant of the motor.

Looking at the efficiency again, we get: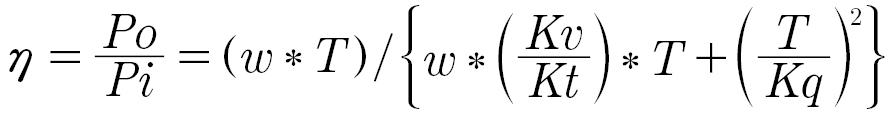

A quick look at the equation says that at zero velocity, efficiency is zero, and will increase with velocity for a given torque level. There is a constraint on velocity, as the back-EMF grows with velocity, and the driver cannot force current into the winding when the back-EMF exceeds the power supply voltage.

For a given torque, the resistive losses term (T/Kq)² will remain essentially constant while the torque producing input power term, w∗(Kv/Kt)∗T will vary directly with speed (w). (This is an approximation as the Kv/Kt ratio includes terms like windage and hysteresis, but for the broad stroke we will ignore these smaller terms for a simpler comparison.)

Taking Torque T out of the numerator and Denominator we get: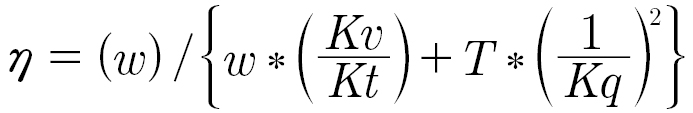

For a given power supply voltage, the maximum no torque speed will be determined by the back-EMF voltage plus the resistive voltage drop of the windings equaling the power supply voltage.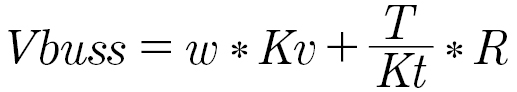

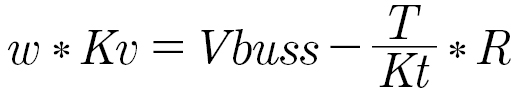
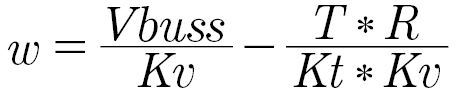
If we approximate Kt ~ Kv just while determining the maximum speed, we get: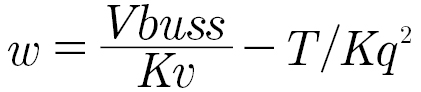

We can see that low velocity constant (and thus torque constant) motors favor higher speeds to obtain a given output power, while high velocity constant motors favor lower speeds. A higher motor quality Kq allows for a higher efficiency at a given torque, given that the motor speed is obtainable for the given motor and power supply voltage.

Indirect Permanent Magnet Motors

The indirect Permanent Magnet Synchronous Motors (IPM or IPMSM) contain soft magnetic materials between the permanent magnets and the rotor-stator gap. The presence of magnetic material between the gap and the rotor magnets enables the gap field strength to be reduced (or even enhanced) by adjusting phasing of the stator current relative to the rotor angle. Adjusting the In-Phase (Id) component of the stator current can subtract from (or with opposite phase add to) the gap flux which produces back-EMF associated with the torque producing Quadrature (Iq) component of the stator flux.

But why would it be advantageous to reduce the torque constant of the motor?

The losses in a motor are mostly determined by speed and by current squared, while the output power is determined by current and back-EMF. The motor driver is also constrained in that to control the current through the motor, the back-EMF needs to be less than the DC bus voltage. The efficiency is thus optimized when the back-EMF is almost equal to the DC bus voltage; this state produces maximum output power versus the losses associated with producing that level of output power. (Note that the driver requires some voltage to overcome the winding inductance so as to achieve the commanded current, and this overhead voltage increases with motor frequency.)

This ability of the IPM motor to vary the gap flux strength allows the voltage constant for the IPM motor to be dynamically varied. This extra degree of control of the IPM motor allows the control algorithm to keep the back-EMF of the motor near the DC bus voltage over a wide speed range, resulting in high efficiency and power levels over this same wide speed range. Contrasted, The direct PMSM motor sees its best efficiency and highest power only when it is operated at nearly at full speed, where the back-EMF for the motor approaches the DC bus voltage.

Reluctance Torque

The Indirect Permanent Magnet motors also normally exhibit what is called Salience—that is the reluctance paths for the direct and quadrature field components are not the same, with the direct component having a lower reluctance. As the field angle is advanced with respect to the rotor—that is the direct flux is increased compared to the quadrature flux, the torque produced by this reluctance variation in the motor is also increased (up to a point), further enhancing the total output torque, adding to the power associated with the quadrature current component and the back-EMF voltage.

There are tradeoffs in the level of salience and the torque ripple for a given motor design, with more salience generally producing more torque but also more torque ripple and higher detent torque associated with the increased salience.

IPM Models

The advantages of allowing the control algorithm to vary the motor torque constant and to utilize reluctance torque also means that the equations for power and efficiency versus speed are also highly dependent upon the particulars of both the motor design associated with reluctance torque and the algorithms and the optimizations chosen. The data presented for the IPM will show the motor performance as measured for a particular IPM (hybrid servomotor) the SilverMax QCI-X34HC-1 is shown both without field weakening and with a particular choice for control of field weakening.

Efficiency at Zero-Speed?

Servos not only move a load at varying speeds, they also can maintain a position. If the output speed is zero, then the output power is also zero, and thus the efficiency is zero. Yet the actual power needed to maintain the position still varies significantly between different motor and controller sets. The “Motor Quality” factor (Kq) is a measure of the losses associated with such a holding torque:

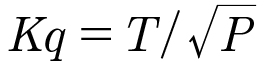
Where T is in Newton-meters, and P is the power loss (P=I²*R) associated with producing the holding torque (T=Kt*I) in watts. Higher torque constants and lower resistance produce higher motor quality values, reducing the power needed to hold a given torque.

The torque constant (Kt) goes up with the number of turns, with gap strength, and with the number of motor pole pairs, while the resistance goes up with the number of turns (for a given cross section times fill factor provided for the winding). The resistance also goes up with the length of the end windings (which add to the resistance but not to torque generation), which vary with the various motor designs.

Comparing Results

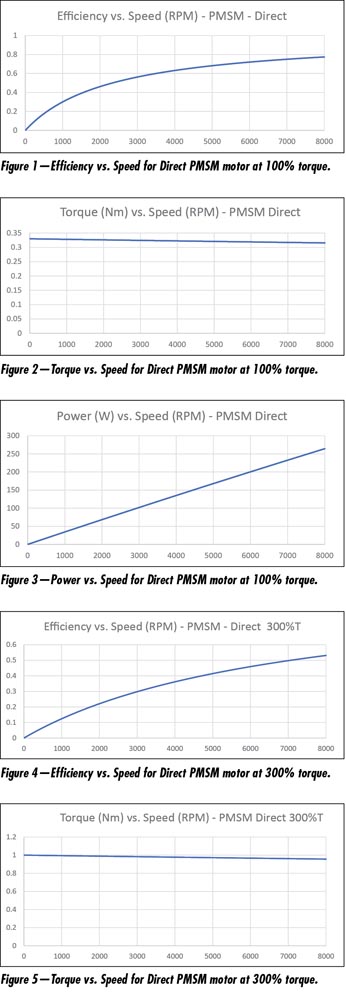
Figure 1 shows the efficiency of a direct permanent magnet synchronous motor versus speed operated at 100 percent torque. The efficiency does not reach 50 percent until the motor is up to approximately 2,500 rpm, with some 75 percent efficiency at 8,000 rpm.

Figure 2 shows the torque is relatively constant over this same speed interval, dropping only about five percent from 0 to 8,000 rpm.

Figure 3 shows the resulting power is nearly linear with speed. A 260 W rated motor at 8,000 rpm only produces approximately 34 W at 1,000 rpm, while wasting nearly 80 for an efficiency of 30 percent.

Figure 4 shows that the efficiency of the same direct permanent magnet synchronous motor only reaches some 50 percent at 7,000 rpm, with only 12.4 percent efficiency at 1,000 rpm.

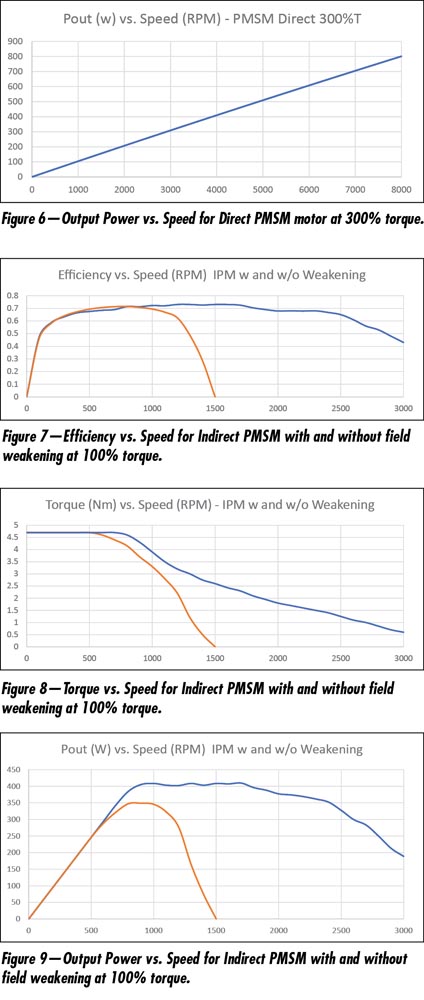
Figure 5 shows the resulting tripling in output torque, with Figure 6 showing the improved peak power, but the losses are above 710 W over the full speed range, which requires a very low duty cycle to prevent overheating.

Figure 7 shows the efficiency for the Indirect Permanent Magnet Synchronous Motor. The broad curve represents the motor when operated with field weakening, while the narrow curve shows the same motor if field weakening is not utilized. The following comparisons will all reference this motor utilizing field weakening. The 50 percent efficiency is achieved at about 150 rpm and remain above 50 percent up to approximately 2,800 rpm, with a broad peak efficiency of 73 percent (including the driver/controller electronics). The losses at full torque at zero speed are just 55 W.

Figure 8 shows a constant torque of 4.7 Nm through about 700 rpm, which then drops down as the field is weakened. The field weakening significantly extends the torque curve as compared to the same motor without field weakening.

Figure 9 shows the power initially is linear with speed, and then remains high over approximately a 3:1 speed range.

Summary

The use of field weakening with indirect permanent magnet synchronous motors allows for broad high efficiency and continuous output power curves. These motors as hybrid servos typically utilize a narrower effective gap which limits the ratio of peak torque to continuous torque to about 150 percent. The direct permanent magnet synchronous motors utilize a larger gap length allowing a higher peak to continuous torque ratio, typically 300 to 1,000 percent, but the resulting heating is 9x to 100x the continuous rating, resulting in low allowable duty cycles. The typically lower pole count face magnet designs are optimized for lower torque higher speed applications, often requiring gearheads for use with belts and lead screws applications, while high pole count indirect permanent magnet synchronous motors (such as hybrid servos) are optimized for direct drive applications.

Applications that require significant holding or low speed torques—such as direct drive of lead screws and belts, and for such applications as lifting or fixturing, precision pumping or milling (other than the spindle) may benefit from the broad efficiency and power curves fan from the IPM motors used in hybrid servomotors.