Dr. Gerhard G. Antony

Introduction
“Mean Time Between Failures” (MTBF) is a very frequent and broadly used reliability measure of components, systems and devices used mainly in conjunction with electrical and electronic equipment.

From the engineering perspective, assessing the life and reliability of products is a vital part of product design, development and selection. Life and reliability of a product are also important characteristics for the user (customer) in comparing gearboxes, for example, to assess their useful value or life for a certain application. The reliability of a product becomes a frequently used marketing and sales feature.

The life characteristics of different products and components depend on a wide range of factors—from type and condition of material used to type of exposure to loads, magnitude of the loads and other effects, such as environment. Products are designed for a certain purpose, function, duty, load, etc.; the life and reliability are of characteristic statistical value and thus can only be approached and assessed by statistical methods.

Today, an increasing number of manufacturers combine a mechanical device, such as a gearbox, with an electromechanical component such as an electric motor, and logic controllers and sensors into a compact, integrated “mechatronics” product. The MTBF value of many electronic components and systems is typically obtainable from the manufacturer. The design life of mechanical components and systems is mainly based on the endurance characteristics of the components relative to the statistical life expectancy under a certain load, such as the L10 design life standard. Can the reliability of a mechanical device such as a gearbox be expressed in terms of MTBF? How many MTBF hours equal a known L10 life? This paper is an attempt to find some answers for these and similar MTBF-related questions.

Life and reliability related issues are based on tests and observation of components applying mathematical (statistical) evaluations and approximations, using appropriate functions and formulas. It is common practice to define characteristic values and choose “scientific” statistical methods to analyze and evaluate them. It is fairly easy to define certain characteristics of a selected number of test specimens by applying statistical methods for an observed population/group and come up with a “scientific, statistical conclusion.” But to have realistic, meaningful conclusions, the definitions and the evaluation methods must be clear and transparent.

This paper is an attempt to express the life and reliability of gearboxes in terms of MTBF without going into an in-depth discussion of statistical methods.

As mentioned, MTBF is a widely used characteristic value to quantify reliability of electronic components and systems, but it is not commonly used for reliability assessment of mechanical components and systems.

For the correct interpretation of the MTBF value it is necessary to understand some basic concepts of probability of failures and the methods of their evaluation.

Failure Rate
The fundamental first step in determining the reliability and life of a component is to observe a representative set of samples—a “population” of components—and to record the failures over a certain time frame.

The collected data will show a certain number of failures over the observed time period. An absolute number of failures has no real practical meaning; it always has to be related to the observed population size. This is expressed by the failure rate.

Failure rate is the relative frequency at which a component or system fails in a given timeframe—i.e., failures/minutes, hours, years or within a certain time-related measure such as distance—i.e., failures/miles (in automotive field); or per operating cycles such as failures in one million revolutions (bearings), etc. As we can see, it is not an absolute number of units failed but rather a relative number, related to the size of the observed tested number of units and population of products (see Fig. 1).

Figure 1—Failure rate, FR.

Indeed, it would be more precise to call it the “relative failure rate” because the value is related to the overall observed population. The rate assumes a value between 0 (0% failures per hour) and 1 (100% failures per hour). This relative failure rate can be recorded at regular time intervals (for determining if and how the failure rate is changing over the life time), or recorded for a predefined period such as the “design life” of the component, assuming that the failure rate is constant during this period.

iPod example (Source: AppleInsider, July 27, 2006—“iPods Built to Last Four Years”): “Apple spokeswoman Natalie Kerris recently told the Chicago Tribune that iPods have a failure rate of less than 5%, which, she said, is ‘fairly low,’ compared with other consumer electronics. However, a survey conducted by MacInTouch last year found that of nearly 9,000 iPods owned by more than 4,000 respondents, more than 1,400 of the players had failed. The survey concluded that the failure rate was 13.7 %, attributed to an equal mix of hard drive- and battery-related issues.”

Remark. Based on the numbers, the actual failure rate should be FR = 1,400/9,000 = 0.155, or 15.5% for the observed time interval. Or, 15.55% – 13.7% = 1.8% failed for some reason other than that listed. Other explanations are also possible, but the survey does not list any.

Is Apple correct with the 5% value over the design life, or are the conclusions of the survey with 13.7% correct?

Here are some important questions before we take sides: Are both talking about the same type of failures? Does Apple consider the necessity to replace the battery a failure? How many units were surveyed by Apple? Is the population of 9,000 samples in the survey representative? (Apple ships in excess of 10 million units a quarter.) What was the real usage time or reference time of both observations? Does the statement “built to last four years” mean four years at 24/7 usage, or, for instance, only four hours a day, six days a week.

None of the above two failure rates gives any specific information about these important basis factors, nor about the conditions under which the data were collected. Let us assume that the survey was based on a 12-hour daily usage over a two-year period; the failure rate should be calculated as:

Equation 1

The example above highlights the main difficulty of the reliability/life calculation and the main source for misrepresentations, namely, the selection of the population, the observed time interval and failure mode, etc.

K-gearbox example. The right-angle, bevel-helical K-boxes have a two-year warranty:

Equation 2

Electronic components and systems such as a simple LED or complex processor chips are used in millions of computers or other devices under exactly defined and controlled conditions (certain voltage and clock frequency rate, temperature, etc.) On the other hand, gearboxes are subjected to a less absolute range, and far less-controlled conditions, loads and environments. Also, the population size is substantially higher for electronic components than for gear boxes. Electronic components are routinely lab tested in high volumes. It is economically impractical to life test a large population of gearboxes or other mechanical components, as well as securing exact same load conditions etc., in order to determine the “mortality” rate. Failure rate values result mainly from “field tests”—observations in real-world applications.

On the other hand, gearboxes are designed based on well-established, statically proven methods frequently regulated by standards put forth by AGMA, ISO, DIN, etc. Many components—bearings, for example—have well-known, statistically proven reliability and life characteristics. The shafts, gears and fasteners, etc., are all based on the endurance limit; there is theoretically no life limitation under the nominal load. This issue will be discussed further in relation to the two proposed methods of gauging gearbox MTBF.

Bathtub Curve
Most components follow the characteristic plot of failure rate over time, as shown in Figure 2.

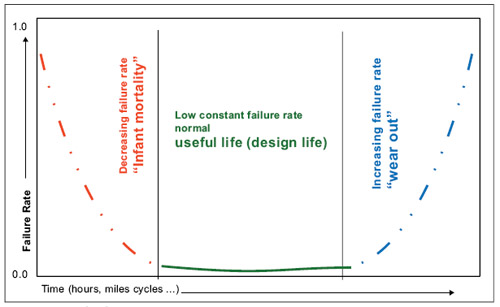
Figure 2—Bathtub curve.

The plotted failure rate over time for most engineered components and systems resembles the form of a bathtub, hence the name “bathtub curve.” It has three characteristic areas—a) the “infant mortality” period, with decreasing failure rates; b) an almost-fl at, nearly constant failure rate period, frequently called the “useful life period;” and c) the increasing failure or “wear-out” rate. The failure rate of living creatures, such as humans, also resembles the bathtub curve.

Electronic components have a very distinctive infant mortality. To minimize this impact on the reliability in practical applications, electronic components are frequently subjected to a “burn-in,” which separates the early failures from the population. On the other hand, the wear-out of solid-state electronic components is far less significant.

Mechanical components, such as gears and gear box components, behave differently in that there is no significant infant mortality. However, the wear-out can be significant. For obvious reasons, and in most practical applications, the useful life period is of greatest interest, not the reliability rate of the infant mortality period or during the period exceeding the design life—namely, the wear-out period.

Probability Density Function (PDF) and Cumulative Distribution Function (CDF)
The probability of an occurrence—or the probability of a certain failure rate—is mathematically de scribed, approximated and analyzed by defining what is known as a suitable probability density function (PDF). The most common and well-known PDF is the normal probability distribution (Gauss distribution) applicable to many natural phenomena (Fig. 3). The area under the PDF—the integral of the PDF—is the cumulative distribution function (CDF).

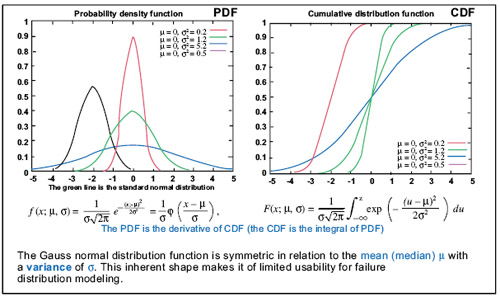
Figure 3—Gauss normal probability distribution function.

And yet, the Gauss normal distribution function is not applicable to “bathtub curve” distributions (Fig. 4).

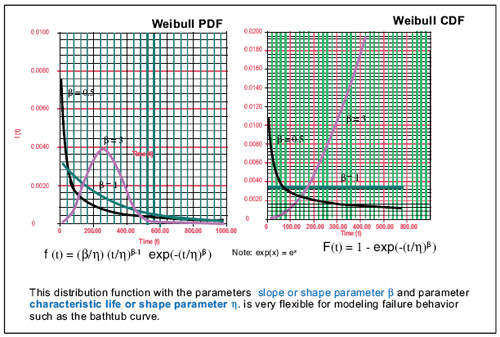
Figure 4—Weibull probability distribution function.

Whereas the normal PDF has the same basic shape for all parameters, the Weibull three- or two-parameter distribution function allows for widely different shapes of PDFs, depending upon the shape parameter. Weibull is well known to gear designers familiar with the bearing design and associated B-life ratings, which suggest that bearings should be compared at a life corresponding to 10% failure probability, or L10 life.

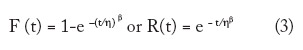
Equation 3

F(t) the Weibull cumulative distribution function CDF (here the widely used two-parameter distribution) provides the probability of failure. R(t) is “reliability,” the complement of F(t) where:

t = failure time,
η = characteristic life, or scale factor
β = shape parameter or slope
e = Euler’s number or Napier’s constant (the base for natural logarithms)

For the three characteristic areas of a bathtub curve:

• The infant mortality—decreasing failure rate of the bathtub curve—corresponds to beta values <1;

• The useful life period—constant failure rate—corresponds to beta =1;

• The wear-out—increasing failure rate—corresponds to beta values >1.

In the Weibull probability plot, which is using an adjusted logarithmic scale, the distribution functions have the shape of a simple line where the slope is equal to the parameter β.

Furthermore, at a time t = η, 63.21% of the population will fail—independent of the β value—since F(t) @ t = η → 1-1/e = 0.6321.

In the Weibull plot, the horizontal line at 0.6231 failure rate has a special meaning (Fig. 5). For failure probability distributions with β =1, the t value corresponding to the intersection point of the F(t) line and the horizontal 0.6321 line can be interpreted as the mean time between failures. Note, this is only correct when β = 1, (constant failure rate) for that useful life region which is the scope of most practical considerations.

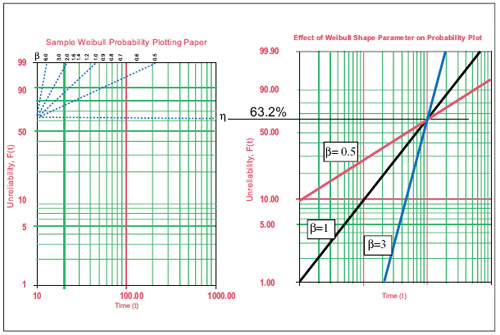
Figure 5—Weibull Plot.

Also note F(t) = 63.21% failure probability means R(t) = 36.78% survival probability.

Mean Time Between Failures Distribution
It should be emphasized that in all practical component (gearbox) applications, the reliability during the useful life (design life) is what matters. This period is characterized by β =1 in the Weibull distribution.

The basic definition of MTBF is simple and logical, evidenced by its comparison to the definition of failure rate FR. The MTBF is the actual reciprocal value of the FR. MTBF = 1/FR (Fig. 6).

Figure 6—MTBF.

Let’s calculate the MTBF for the two examples presented above.

iPod example:

Equation 4

Obviously, we cannot expect that an iPod will last 56,314 hrs, or an equivalent of over six years of flawless operation.

K-gearbox example. Right-angle, helical bevel K-boxes have two-year warranties:

Equation 5

Here again the expectation that a K-box will last about 67 years under continuous operation would be a false interpretation of the MTBF value. But in comparing the two values, we can certainly say the K-box is about 10 times more reliable than an iPod.

The above examples calculated the MTBF based on field survey data and using a number of assumptions. As mentioned regarding failure rate, the population size, the observed time frame, consistency of loads and real operation time all influence the MTBF.

Ideally, lab tests should be conducted on a large population of products, replicating the same conditions, in order to have an objective, comparable and representative MTBF value. However, it is not economically feasible to carry out extensive lab tests on products like industrial gearboxes. Too, the expense of running lab tests on hundreds of gearboxes for the period of their design life is not justified, even in high-volume products such as automotive transmissions.

Gearbox MTBF Determination
Obviously, the life and reliability of a mechanical system such as a gearbox also depend on the life/reliability characteristics of its other parts at a certain defined design load. Since testing a large number of gearboxes is not practical, the goal would be to determine MTBF values based on the design parameters and reliability characteristics of its components.

The main load-carrying components of a gearbox are the gears, shafts, shaft/hub connecting devices and bearings. Other secondary parts such as seals, fasteners, etc., are not directly involved in the torque transfer. Therefore their influence on the gearbox life is practically impossible to quantify simply from the design data alone.

Gears and Shafts
Remember, since products are designed and made for certain nominal loading (usage) conditions, the MTBF generally is referenced to these “normal” conditions.

Gears, shafts and hub/shaft connections are generally designed based on endurance (fatigue characteristics) design standards. These components should be selected and shaped to endure under the “nominal,” i.e., rated, load conditions of unlimited load cycles. The stresses under the nominal load—the bending stress at the tooth root, for instance—must be below the endurance limit. The endurance limit values in themselves are not exact; they are statistical. For this reason the design standards include a number of sizing factors (size, surface, life factor, etc.) to adjust the endurance limit to in effect err on the safe side. Since they are based on endurance limits (theoretically unlimited life), it can be said that component designs based on endurance limits will not influence the MTBF. However, in real-world applications these components do fail, but mainly because overloads occur if, for example, they are loaded beyond the design specifications.

If the loads are above the nominal value, even if only occasionally, the life of these parts is limited. If the number, duration and magnitude of the load cycles above the nominal load are known, it is possible to estimate/approximate the life by using calculation methods such as the Palmgren-Miner linear damage hypothesis.

Bearings
Rolling element bearings, the other main component of a gearbox, have a different life characteristic in that they are not selected based on endurance limit, and their life is inherently limited. Their selection/design is based on standardized calculations rooted in statistical evaluations/methods. This fact makes it possible to approximate the life/reliability equivalent of bearings in terms of MTBF. That said, two alternatives are suggested here for the determination of the MTBF of a gearbox.

Proposed Alternative 1: Gearbox MTBF determination—based on warranty/repair figures.

The calculated MTBF value of gearboxes based on:

a) Observation time equal to the warranty time

b) Population equal to average amount shipped during the observation time

c) Number of warranty returns, or the percentage of the warranty returns as a number of failures, is a valid approach to determine the MTBF. Most manufacturers have these or similar values, typically established quality control personnel or a management system such as ISO 9000 (see example K-box above).

To have an honest, comparable MTBF value it would be beneficial to develop certain guidelines and standards for the collection of the above-mentioned data.

Proposed Alternative 2: Gearbox MTBF determination—based on L10 life. As discussed above, with Weibull distribution function at β = 1, the η value corresponds to the MTBF. The key mechanical components of countless mechanical systems are often the rolling bearings, and the L10 life of bearings is well-defined. Selection of bearings is based on this value. If, for example, a gearbox has bearings designed/rated for a 100,000-hrs, L10 life, that means there is a 10% failure probability or, conversely, a 90% reliability probability.

Discussing the Weibull plot at β=1, we concluded that the MTBF value corresponds to a 63.21% failure probability/36.78% reliability probability.

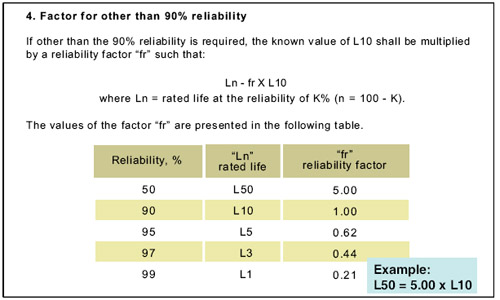
Ln values (L1 to L50) for bearings are listed in terms of the L10 in engineering literature, such as Ln = FR × L10. This is based on many years of tests and field data.

While the literature lists values up to L50, no explicit L63.21% value is found. However, extrapolating graphical curves Ln = f (L10) indicates that the FR value at 63.21% reliability is around 8.5.

We can therefore conclude that in (gearbox) systems where the rated life is mainly based on the L10 bearing value, the MTBF is equal to: MTBF = L10 × 8.5.

But with that, it must be remembered that in many gear boxes the bearings are considered as wear parts, which can and should be periodically replaced. Using existing predictive maintenance techniques, bearings can be kept in operation far longer than their designed L10 life. Predictive maintenance can also indicate when to replace a bearing, regardless of its designed L10 life, thereby avoiding consequential damage to the gears and other components. The above approximation of the overall gearbox MTBF, based on the L10 value, is rather conservative. In many gearboxes, the bearings are not actively involved in the torque transmission, but still have the vital function of supporting the torque-transmitting components. On the other hand, with some gear types such as epicyclical or planetary gears, the bearings are directly involved in the torque transmission, as with the needle bearings of planet wheels.

Example: PLE Planetary gear head. The needle bearings of a PLE planetary gearbox are designed for 30,000 hrs. L10 life at rated torque. The gears are designed based on the endurance limit at rated torque. In planetary gears, the planet gear bearing is the vital part in the torque transmission, subjected to loads proportional to the transmitted torque. Thus the MTBF of the PLE gear head can be calculated as:

MTBF = 30,000 × 8.5 = 255,000 hrs

Conclusions/Suggestions
MTBF is a frequently used value to quantify reliability of electronic components and systems. It can certainly be used to state the reliability of mechanical components and systems if the basic rules are followed and interpreted correctly.

The proposed two alternatives determine the MTBF of a gearbox using data which, in many cases, are readily available to the gearbox manufacturer and designer. However, the first suggested method—based on warranty figures and field tests—provides a more balanced and complete realistic reliability assessment than the suggested second alternative, based on L10 bearing life.

As a result, the MTBF value determined by methods one and two for the same gearbox will differ significantly, in most cases. Therefore, when listing an MTBF value, it should be noted which approach is used. The bearing base method is only recommended if field test-based values are not available.

It would be beneficial to develop and publish appropriate AGMA guidelines, recommendations or standards to make the used data consistent, thus making the MTBF values of different gearboxes comparable.

References
1. Abernathy, R.B. “The New Weibull Handbook.”

2. “Reliability Basics,” Reliability HotWire–The Magazine for the Reliability Professionals, Issue 14, April, 2002.

3. Wilkins, Dennis J. “Bathtub Curve and Product Failure Behavior,” Reliability HotWire– The Magazine for the Reliability Professionals, Issue 22, December, 2002.

4. Speaks, S. “Reliability and MTBF Overview,” VICOR Reliability Engineering.

5. Shigley, J.E. “Machine Design,” McGraw-Hill, NY.

6. Dudley, D.W. “Gear Handbook,” McGraw-Hill, NY.

7. Dudley, D.W. and H. Winter. “Zahnraeder Berlin,” Springer Verlag.

8. Nieman G. and H. Winter. “Machine Elements,” Springer Verlag.

9. www.efunda.com, “Engineering Fundamentals.”

10. www.weibull.com, “Reliability Engineering and Weibull Analysis Resources.”

11. ANSI/AGMA 2101 D04, “Fundamental Rating Factors and Calculation Methods for Involute Spur and Helical Gear Teeth,” Metric Edition.

12. ANSI/AGMA 2001 D04, “Fundamental Rating Factors and Calculation Methods for Involute Spur and Helical Gear Teeth.”

Dr. Gerhard G. Antony possesses more than 30 years’ experience in electromechanical and power transmission and automation. He earned his MS and PhD in engineering at the University RWTH-Aachen, Germany. After working at the university in education research and consulting, he went on to work in a wide range of positions and projects with and for companies such as SEW-Eurodrive, RACO International and Sumitomo PT. He currently serves as general manager of Neugart USA LP and is president/owner of the engineering firm i.MTRDC LLC. He has authored more than 25 papers in his field of concentration.

Printed with permission of the copyright holder, the American Gear Manufacturers Association, 500 Montgomery Street, Suite 350, Alexandria, Virginia 22314-1560. Statements presented in this paper are those of the Authors and may not represent the position or opinion of the American Gear Manufacturers Association.