Open Loop Step Motor Error Sources - What Closing the Loop Corrects
Reducing Plant Downtime
Win-911 Examines Critical Role of Remote Alarm Notification Software
Two-Phase Hybrid Step Motors — also known as transverse magnetic flux permanent magnet motors — provide a very cost-effective and simple motion control solution. However, they have a number of inherent errors when operated open-loop or quasi-open loop (which some manufacturers call closed loop). We will go through several of the dominant error sources when using these motors, and comment on how the errors are overcome by true servo operation of these motors.
Previous articles have highlighted the difference in the laminate design that determines whether the motor is optimized for microstep operation or for full step operation. In this article we will focus on the microstep optimized laminate hybrid step motors.
Degrees of Servo – None to Full
First a quick definition of the terms we will use to describe closed loop “levels.” This was covered in detail in a previous article, so I will keep this section brief. The basic step motor is considered open loop — there is no feedback of position. The first level of closing the motor uses a typically lower resolution encoder to adjust the stepping rate so as to keep the motor error to usually no more than either plus-or-minus 1 full step or 1.5 full steps (according to the patent). This helps the motor provide high torque without loss of steps, but it does address the resonance problems (see below); I refer to this as quasi-closed loop.
Another level of closed loop observes the motor current versus applied voltages to estimate the rotor position using Kalman estimator techniques (or similar). These indirectly are measuring the back-EMF of the motor to determine position by measuring how the back-EMF affects the measured current. They are effective at higher speeds where there is sufficient back-EMF, but they typically revert to open loop step operation below some minimum speed, and are not able to correct position errors below the minimum speed. Then you have full servo, which measures the rotor position and can control the motion from zero speed to the full motor speed.
Motor-Related Errors
Even within the microstep laminate variety of motors, there are still different optimizations for trading off detent torque versus maximum holding torque. For high accuracy, the detent torque needs to be minimized to reduce the magnitude of the error it introduces, and the harmonic content of the detent torque also needs to be minimized to help prevent “snapping” from one pole to the next pole. If the detent torque has significant harmonics, the rapid change in detent torque versus angle will cause vibrations and stopped position errors as the motor goes over these “speed bumps.” An earlier article provided techniques for measuring harmonic content of the detent torque.
In addition to the errors introduced by design choices such as detent torque and harmonic content, there are also manufacturing tolerances. These include the shape of the tooth as actually produced by the die, distortions in the laminate metal produced by the stamping process (which affect the grain structure and thus the magnetic properties of the steel adjacent to the cut), and the balancing of the anisotropic nature of the rolled steel used for the laminates (grain direction affects the magnetic properties). Finally, the degree of the centering of the rotor within the stator and of the rotor about its bearings affects accuracy of the motion.
Looking at a series of the specifications provided by multiple step motor manufacturers — and not all provide accuracy specifications — the specifications are called out as ±3% to ±6% non-cumulative error by different vendors; others call out a step to step error of .09 degrees for a 1.8 degree step motor (±5% of a step). This is the best expected open loop accuracy for the no-load condition at the full step location, which hides the effect of detent torque. Thus even with perfect microstepping current control, the expected error from the unloaded motor is not better than 1/20th of a step. And real position error only gets worse as we start adding any load and friction to the motor!
Driver-Related Errors
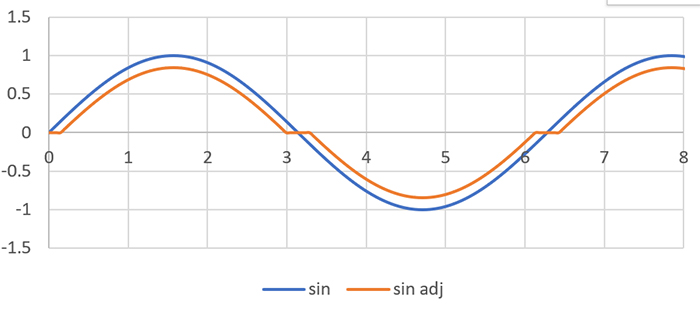
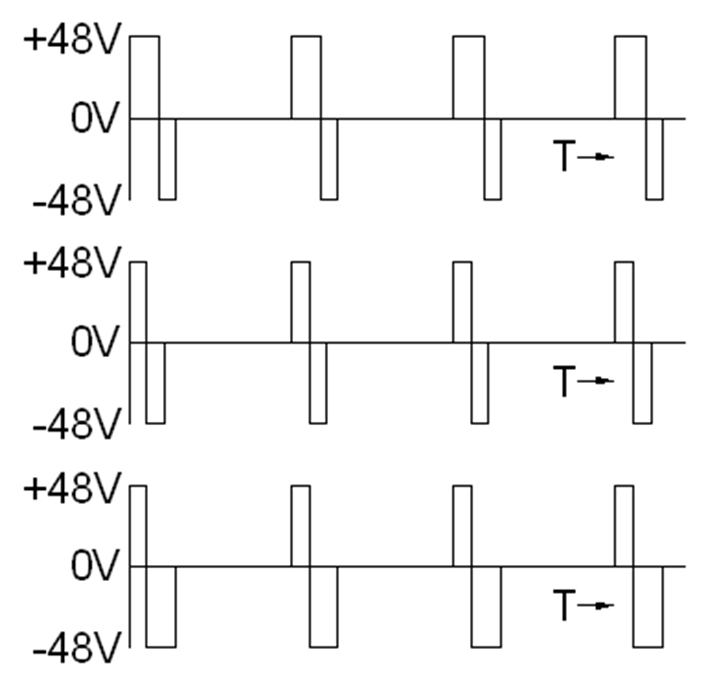
The motor manufactures typically specify resistance as ±10% at room temperature, with inductance typically specified to ±20%. A good current mode driver should compensate for most of these differences, at least for the full step locations. Many recirculating drives have problems controlling the current near zero current due to cross over distortion. Two issues that contribute to this error: dead-band and minimum duty cycle. Dead-band arises from the minimum allowed time between turning off the upper transistor stage and turning on the lower stage (or Vise-versa) that is allowed so as to prevent shoot-through current (current which flows through both high-side and low-side transistors — which generates much EMI and can destroy the driver). On a PWM controlled stage, the dead-band reduces the effective PWM signal so that the overall current is reduced towards zero. This reduces both the peak expected current (which can be easily corrected with a PI current controller) and the current near the cross over (which is not as easily corrected if the commutation rate is faster than the PI loop). The dead-band shown corresponds to 200nS of dead time with a 25kHz chopping rate for a 2.5v motor running from a 48v supply. This level of error represents 0.16 degrees or about 1/8 of a step (Figure 2). QuickSilver compensates for dead-band, which significantly reduces the position offset when operating in open loop, and smooths the resulting motion when operating in closed loop.
Another significant distortion inducing limitation is the minimum allowable on-time for the driver. The transistors take a finite time to fully turn on before they are switched off again. The minimum on-time can be on the order of 1uS for some common drivers. For a 25kHz chopping rate (40uS per cycle), this is 2.5% on minimum. With a 48v power supply used with a 4 amp 23 frame motor — typically having a .5 ohm winding resistance, the minimum on time produces 1us/40us*48v = 1.4v to the winding. With a .5 ohm winding this corresponds to 2.8A. To reduce the current to a lower level, the chopper drive must either drop out of recirculate mode (which makes the average current much less than the peak sensing used in the control loop and increases the ripple current), or it must increase the time between pulses which allows the chopping frequency to enter the audible frequency range causing an audible squeal. The large minimum current also causes a significant step in position as the current reverses as the current jumps from the minimum positive current to the minimum negative current when using a typical current sensing recirculate scheme. QuickSilver addresses this by using a gated anti-phase technique in which a controlled reverse pulse period is used with the main forward pulse to allow a smooth transition from positive to negative current while keeping the motor drive active (avoiding decay mode and its large ripple currents). The gated anti-phase technique also allows for excellent control of the current in all four quadrants of operation — that is both when using the motor to accelerate the load (supplying power — 1st and 3rd quadrant) and when using the motor to decelerate the load (absorbing power — 2nd and 4th quadrant). Typical peak current sensing recirculating drivers are not as accurate in the 2nd and 4th quadrants controlling the current while decelerating the motor.
Additional Motor Variances
Additional motor manufacturing variances that can affect microstep accuracy include the balance of A and B windings. If the rotor is not centered on the stator, the average gap between the rotor to the stator associated with each phase may not be balanced. This imbalance may cause the back-EMF of phase A to vary substantially from that of phase B. The back-EMF of the motor directly relates to the torque constant (Newton meters per amp) of the motor, so this affects both the pointing accuracy and the smoothness of rotation of the motor. Closely related is the quadrature of the two phases, which can also be affected by rotor to stator alignment. Normally, the back-EMF of the two phases are offset by 90 electrical degrees so that the optimal waveforms are sine and cosine currents. If the rotor alignment is not well centered, this angle between the phases can vary, causing the motor angle to not be accurate, and the torque generated to vary as a function of motor position. The balance and quadrature are errors are usually fairly low, but rough handling of a step motor can significantly impact these by misaligning the rotor centering to the stator. Closed loop operation can significantly compensate for the motor imperfections to obtain smoother and more accurate motions.
Hysteresis
One effect that remains in open loop operated motors is magnetic hysteresis. The magnetic field from the stator does not drop to zero when the current drops to zero, but rather the stator remains partially magnetized. When the current is applied in the opposite direction with sufficient magnitude to reverse the hysteresis, the motor will take a larger (micro) step. This shows up as a larger motion as the motor passes through the full step locations as these locations correspond to where one of the two phases crosses through zero current. QuickSilver driver techniques also combat the hysteresis effects to smooth the motion both when operating open loop and closed loop.
Torque Generation
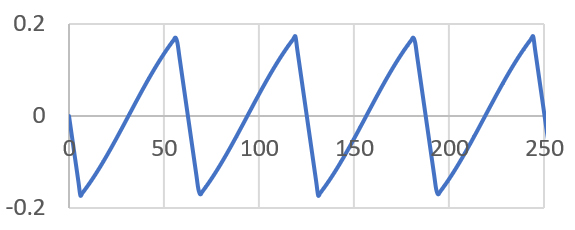
The step motor only generates torque when there is a an error angle present. Zero error (difference between the magnetic angle presented to the motor via the two motor phase currents and the mechanical angle of the shaft). The electrical cycle repeats every 4 full steps (7.2 mechanical degrees for a 1.8 degree stepper). If the rotor is slightly ahead of the magnetic angle, then a negative torque is generated (Figure 4 shows normalized torque versus error angle in steps). A negative error angle produces a positive torque - as long as the error is less than 2 steps. The maximum torque generated is at one full step error and going beyond plus or minus 1 full step of error and the torque starts falling. Going past 2 full steps and the torque pushes the rotor further away until it comes to a rest again at 4 full steps (or a multiple of 4 full steps) from the targeted position. This is how open loop step motors loose steps.
Of note is that a load requiring 50% of the motor torque forces an error of 30 electrical degrees or 1/3 of a full step. Friction is only overcome if the error angle is sufficient to generate torque sufficient to exceed the friction magnitude. Any ringing may end up on either side of the zero point according to which side of the ringing waveform ended up with just enough friction to “capture” the rotor and stop motion. So micro-step drives, even if there are many fine divisions very accurately controlled, still may have significant following and stopping error due to load forces and friction.
True servo closed loop systems measure the error and apply appropriate current at the needed angle to move the rotor to the desired position. Quasi-closed loop steppers only prevent losing multiple steps, but otherwise still have the problems with load and friction induced errors.
Resonances
Low frequency resonance arises from the torque curve of the motor (which approximates a K-theta rotary spring) interacting with the rotary inertia of the motor (and the load). This sets up a rotary pendulum. When the stepping frequency of the motor excites the resonance of this pendulum, it causes an oscillation to grow. At some frequencies, the motor ends up moving in the wrong direction as the next step is applied, resulting in 90% or more loss in available torque and very rough motion. Lost steps or total loss of synchronization may happen if the load torque exceeds the available torque. It is also possible to excide other modes where the motor operates at a fraction or a multiple of the drive frequency due to the non-linear torque curve causing non-linear mixing of the applied sine wave with the back-EMF of the motor. You may get motion but at the wrong speed or the wrong direction!
The low frequency resonance issues are still present with quasi-closed loop (error limiting systems), except that they will not lose steps. True closed loop system keep the motor phase angle at either +1 step or -1 step and vary the current magnitude to get the required torque. By keeping the motor at the peak of the torque curve, the motor efficiency is maximized, while also making the derivative of torque with respect to angle zero. The system is no longer a 2nd order oscillatory system, but rather a damped first order system: the motor runs cooler and smoother!
Mid-frequency resonance is not a true resonance, but rather a limit cycle oscillation. When using a peak current controlling recirculating drive, there is a critical frequency where there is not quite enough on time for the controller to bring the current to the desired level in the provided time. The back-EMF of the motor and the motor inductance resist the rate of current change needed. At this speed, the drive is no longer able to reach the full current, and so the drive switches from acting like a current controlled drive with a low phase lag to being a voltage driving the inductance of the motor with a 90 degree electrical lag. The reduced drive angle causes the motor to slow down slightly, which then allows the current control to engage, only to speed up and no longer reach full current. The resulting instability due to alternating between a current control and voltage control causes a speed oscillation that appears to be a resonance. Closed loop control of the motor current using a knowledge of this issue is able to suppress this limit cycle allowing for a wide range of speeds with full available torque and significantly smoother motions.
High Inertias Interacting with Low Damping Current Drives
Dynamic errors can be very problematic with high inertia loads. Even with careful ramp generation to attempt to minimize the ringing, a load can oscillate about the commanded trajectory by ±½ step over the duration of even an extended move. For example, this type of oscillation has been noted to continue almost unabated over a 16 second spin of a high inertial load. The oscillation remained over the full spin time and likely would have continued if the duration of the spin had been longer. This continued oscillation is due to the very low damping associated with a current mode driver interacting with a step motor.
Additional errors can occur if the motor is operated near resonant frequencies of the motor. Avoiding resonance involves trying to jump through the problematic resonance frequencies to keep from building up oscillations, but that may not be the motion needed for the apparatus!
Many microstep controllers also have a problem at higher speeds as they cannot update the requested phase fast enough to hit all 256 micro-steps of a high-resolution microstep controller. They end up having to change modes at different speeds which can give rise to torque hiccups at these transitions. The chopping rate may also not allow the driver to actually hit the intervening micro-steps as the chopper drive may not be in the drive mode for several of the intervals when chopping at a nominal 25kHz to avoid excess heating.
QuickSilver adds significant damping to the system both in the driver algorithms which can modify the electrical impedance seen by the motor and by adding damping terms to approximate a viscous inertial damper to the control system law. We also use a fixed sampling system to handle the commutation without jumping modes like the micro-step controllers require.
The inherent damping of a step motor with a low impedance drive can be easily seen by shorting the leads of the step motor and attempting to rotate the shaft. A true current mode driver has a very high impedance which can impart torque, but does not interact significantly with the motor back-EMF. A controlled impedance drive algorithm can provide good 4 quadrant performance, high efficiency, and significant damping to allow for very smooth operations even with a widely varying load.
The ultimate performance of these motor varies greatly with the drive and control algorithms and circuits. Motor efficiency, acoustical noise, vibration, damping and available torque-speed curves can all be significantly improved by the appropriate algorithms!