Rolling Bearing Performance Rating Parameters Review and Engineering Assessment
Rolling Bearing Performance Rating Parameters Review and Engineering Assessment
Abbrevations


Introduction
The main function of rolling bearings is to support load and transmit rotational movement with minimum energy loss. In order to achieve this, bearings are manufactured with particularly good quality fatigue resistance materials, proper design and tight manufacturing tolerances. Particular emphasis is put in both the macro, and micro geometry of the working shapes and surfaces of the raceways. Rolling bearings come in many types and sizes as ball and roller bearings for radial and thrust loads. For many years, the selection of the proper bearing for an application has relied on the matching of two main aspects:
- An adequate definition of the performance rating parameters related to the actual manufacturing process and quality of the bearing, usually performed by the bearing manufacturer.
- An adequate definition of the operating conditions and of the safety factors of the particular application, usually performed by the application engineer.
The first aspect requires: i) a quality control and assurance system during manufacturing process, and ii) a methodology for the assessment and validation of the performance parameters that are applied to bearing products. Usually this is done using load rating models that are validated by dedicated tests of the product.
The second aspect requires measurements, experimentation and good engineering knowledge of the specific application. This includes: i) dynamic load variations and transient conditions, and ii) the effect of the environment that may influence the performance of the bearing in use.
The current paper focuses on the first aspect of the engineering selection process, critically reviewing the methodologies that are applied in bearing performance rating and their relation to bearing manufacturing quality and experimental validation.
International standards are very important here. A frequently employed standard is the ISO 281 (Ref. 1) which establishes the definitions of the dynamic load ratings of rolling bearings. This standard provides the methodology for the simple calculation of dynamic load capacity of rolling bearings based on the main geometrical parameters of the bearing and standard high quality material.
However, the standard has important limitations that users often overlook. The standard applies only to good quality bearings. In other words, bearings that represent the “status of the art” of rolling bearing manufacturing technology. In practice, this means, by quoting the standard: “rolling bearings manufactured from contemporary, commonly used, high quality hardened bearing steel, in accordance with good manufacturing practices.” Unfortunately, no quantitative measure of this definition of bearing quality is given in ISO 281. This, in turn, let the undifferentiated application of ISO performance parameters and dynamic load ratings to the large variety of rolling bearings that are produced today.
Verification of the ISO 281 dynamic load ratings would require the use of proper, statistically meaningful, endurance testing of rolling bearings population samples to determine the life L10. However, standards of bearing endurance testing for the verification of dynamic load ratings of rolling bearings are not part of ISO or any other standard. This leads to the present situation in which bearing manufacturers typically apply ISO ratings to describe the performance of their products. However, only very few, generally well-established companies with a long tradition in quality and testing, actually verify the performance parameters of their products by means of dedicated endurance testing (Ref. 2).
Today mechanical engineers have to decide choosing a bearing among different manufacturers. In some cases, significantly different load ratings for seemingly similar bearings type and size are given without a clear explanation of the reasons behind the applied load ratings or whether or not these values are routinely supported with a quality control system and endurance testing practices. This situation is further complicated by the fact that, given the very high costs involved in bearing fatigue life testing, the results of endurance testing are usually proprietary information of the bearing manufacturer that is not released into the public domain.
This paper addresses these issues by reviewing the calculation methodologies of the most relevant load rating parameters of rolling bearings. Their definition, origin and significance in terms of fatigue life of the bearing are clarified. Verification methods of these performance parameters are also discussed. This includes the required endurance testing and the basic statistics that are used in this field.
Objective of this Paper
The intent is to critically review the most important rating parameters used in the prediction of rolling bearing performance. To discuss their origin, definitions and significance in terms of fatigue life of the bearing. To clarify their limitations and applicability in bearing selection and machine design.
Bearing life rating parameters. Life in rolling bearings depends on many parameters and application influence, like lubrication conditions, sealing effects, solid and liquid contamination, variable loading and speed conditions, etc. However, to select the size of a bearing, rating life calculations are used. The standard ISO 281 (Ref. 1) describes the modified bearing rating life with 90% survival probability as:
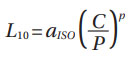
Where L10 is the bearing rating life for 90% survival probability, C is the dynamic load rating, P is the equivalent load in the bearing and p is a constant exponent that depends on the bearing type (3 for ball bearings and 10/3 for roller bearings). The life factor αISO is given in (Ref. 1) in dedicated charts and equations for the different lubrication and contamination conditions of the bearing. However, the basic theory comes from Ioannides et al. (Ref. 3) where a more detailed description of this life factor is given. Therefore, herewith it will not be denoted as αISO but (as in (Ref. 3) as αSLF to avoid confusion with the standard:
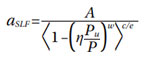
With, A being a scaling constant, Pu is the fatigue limit load (Cu in ISO 281 nomenclature), is a stress penalty factor (environmental factor) described in (Ref. 2) as η = ηa ∙ ηb ∙ ηc. In which: ηa is a macro-scale “parasitic” stress aggravation affecting the bearing. This may be originated by: i) bearing mounting, ii) hoop tension or, iii) residual stresses from heat treatment and manufacturing processes. The factor ηb is the lubrication factor that depends on the lubrication quality κ, as defined in the ISO 281. Finally, the contamination ηc (in ISO 281 nomenclature ec) is the stress penalty for stress concentrations developed on the bearing raceways due to solid particles contamination denting. The remaining constants of Equation (2) are the w exponent (related to the bearing type), the fatigue exponent c of the stress-life equation, and e that is the Weibull exponent.
From these two equations, the main bearing life rating parameters that depend (or may be affected) by the bearing geometry, material properties, manufacturing process and quality are C, Pu and ηa. Another important parameter, related to the maximum load safety of the bearing and its performance under low cycle fatigue, is the static load rating C0 which will be discussed in detail later in this paper.
Dynamic Load Rating
This parameter (C) was originally invented by Lundberg and Palmgren (Refs. 4–5) when they introduced the equation of the basic rating life of rolling bearings:
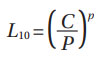
Lundberg and Palmgren, in their work, refer to (C) as the basic dynamic capacity of the bearing. It was defined at that time (Ref. 4) as: “the radial load (or thrust load) which 90% of the bearings can endure for one million revolutions under certain specified conditions of operation.”
ISO 281 (Ref. 1) re-writes this definition, depending on weather the bearing is radial or thrust, using the following terminology: Basic dynamic radial/axial load rating: “Constant stationary radial/concentric-axial load which a rolling bearing can theoretically endure for a basic rating life of one million revolutions.”
ISO 281 (Ref. 1) gives also specific equations to calculate (C0) for each bearing type (radial or thrust, ball or roller) which are obtained from the general methodology originally developed by Lundberg and Palmgren (Refs. 4–5).
General methodology for the calculation of (C). Hereafter the study follows the same methodology of the original work of Lundberg and Palmgren (Ref. 4); this is done to arrive at an estimation of (C) before any approximations or simplifications are introduced into the equations. From the original work of Lundberg and Palmgren (Ref. 4), the dynamic load rating (C) of a rolling bearing can be calculated directly following the analytical method described in the following equations. The analysis can start by considering Equations (47) and (48) from (Ref. 4). Using the same basic nomenclature as in (Ref. 4) these equations are hereafter re-written as Equations (4) and (5).
For point contact (ball bearings).
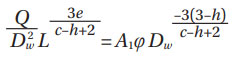
For line contact (roller bearings).
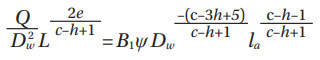
Furthermore, with the basic notation as from (Ref. 4), T = τ0/p0, ε = z0/α p0 = maximum Hertzian pressure. T0, ε0, T1, ε1 are functions of T and ε for α/b = 0 and α/b = 1, respectively (a along the rolling direction, minor semi-width).
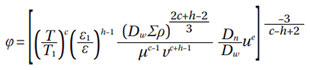
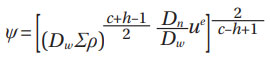
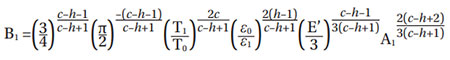
With N = uL, ∑ρ = curvature summation used in contact theory, v, μ Hertzian functions related to the elliptical integrals. A1 is a proportionality constant determined experimentally from endurance testing of representative populations of rolling bearing samples. A1 is given in the original work (Ref. 4), with bearing loads expressed in (kg) units. For bearing loads given in (N) and bearing dimensions in (mm), consistently with Equation (7) of (Ref. 6) (pages 8 and 11), one gets A1 = 1101.87 and B1 = 1141.096.
Notice that A1 and B1 need to be further updated to account for the factor bm that was introduced in ISO in 1990, and is used in the current version of ISO 281 (Ref. 1). This will be further discussed in the next section. Detailed parameter description of Equations (6) and (7) are included in Appendix A.
It follows that if Qc is the rolling contact load for the calculation of the dynamic load rating, from the load rating definition, the life is L = 1 million revolutions, then Equations (4) and (5) yield:
For point contact (ball bearings).
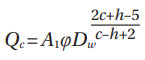
For line contact (roller bearings).
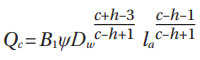
Based on equations (89) and (95) (Ref. 4), for the inner and outer bearing ring (inner – ι, outer – e) the bearing external load P can be related to the maximum contact load Qc as,
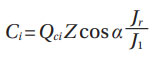
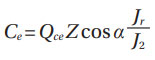
Where Jr is the Sjövall’s radial load distribution integral.
Calculated values of this integral are given in Table 3 of (Ref. 4) depending on the bearing clearance parameter ε. Assuming a bearing with zero clearance, thus (ε = 0.5) one has the following values: Jr = 0.2288 for a single-row radial ball bearing and Jr = 0.2453 for a single-row radial roller bearing. The parameters J1 and J2 are load distribution factors that account for the load variation in the rings due to bearing rotation. For instance, refers to the rotating ring and to the stationary one. Reference 4 in Table 10 gives values for these factors as a function of the bearing clearance; for zero clearance (ε = 0.5) and single-row ball bearings J1=0.5625, J2=0.5275, and for single-row roller bearings J1=0.5965, J2=0.6814.
Finally, from Equation (87) (Ref. 4),
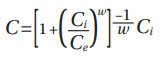
Equation (11) represents the most general way of calculating the dynamic load rating of a bearing without using further simplifications, as they have been used (Ref. 4), or the additional modifications formalized in the ISO 281 (Ref. 1) standard.
All the equations discussed above were programmed in a computer code. Calculations were performed to directly determine the value of (C) for radial ball and radial roller bearings of different size and type.
ISO methodology for the calculation of (C). The ISO 281 (Ref. 1) methodology for the calculation of the dynamic load rating (C) also introduced further simplifications of the original Lundberg and Palmgren (Refs. 4–5) method, as described above; this is the most widely used methodology in industry. The main simplifications introduced by ISO are related to the calculation of the radial and axial Sjövall’s load distribution integrals Jr and Ja. Some numerical values to the exponents c, h, w, ℯ were also re-defined. Finally, the values of some complex type of functions are given in the form of tabulated values, or as simple heuristic functions to achieve standard ISO equations that can be quickly calculated.
In addition to this, the bm multiplication factor was introduced in ISO in 1990. Therefore, in order to reflect the original model results, as given in (Refs. 4–5), the multiplication bm should be set as equal to one. This factor is defined by ISO 281:2007 (Ref. 1) as: “rating factor for contemporary, commonly used, high-quality hardened bearing steel in accordance with good manufacturing practices, the value of which varies with the bearing type and design.” This factor has been used in the past to increase the dynamic load rating in order to reflect technological improvements of all kinds (Ref. 2) (material, design and manufacturing) — as shown first in the implementation of ISO 281 — 1977. A summary of the ISO equations for individual radial bearings is provided below. From now on, the focus of this paper will be on radial bearings only.
Radial ball bearings.
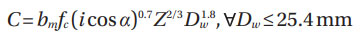
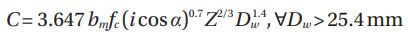
Where 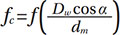 is given in Table 2 of (Ref. 1), while Table 1 of (Ref. 1) gives bm as 1.1 and 1.3.
is given in Table 2 of (Ref. 1), while Table 1 of (Ref. 1) gives bm as 1.1 and 1.3.
Radial roller bearings.
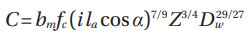
Where 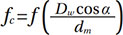 is given in Table 7 of (Ref. 1), while Table 1 (Ref. 1) gives as 1.1 and 1.15.
is given in Table 7 of (Ref. 1), while Table 1 (Ref. 1) gives as 1.1 and 1.15.
As discussed (Ref. 7) using the above equations and a simple Vernier caliper, it is possible to quickly verify the dynamic load rating of any bearing that can be disassembled and measured. Notice that Equations (12) and (13) require all distance in [mm] with the resulting load C in N.
Calculation examples of dynamic load rating. In order to show the results from Equation (11) and to compare it with the ISO methodology, a few simple bearing cases are selected for calculation purposes. A summary of the cases and main geometrical parameters are summarized in Table 1.
The cases of Table 1 have been calculated using Equation (11) and also Equations (12) and (13). The results are compared with the catalogue values of three well-stablished bearing companies; Table 2 shows this comparison. The reader should also be aware that the values quoted by the bearing manufacturers normally are rounded off using Renard series, which may introduce variability of up to ±4% from the exact calculated value.
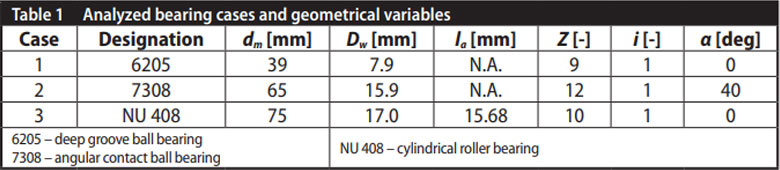
Table 2 shows that, in general, calculated values with the equations from the ISO standard, Equations (12–13) are slightly higher values than Equation (11) — except for case 3, where the opposite occurs. This generally matches well the increase in the factor by ISO over the years. For instance, at the present time the standard (Ref. 1) gives bm = 1.3 for cases 1 and 2 and bm = 1.1 for case 3. Multiplying the values given in Equation (11) by these factors produces very similar values as the ones given by Equations (12–13). For the case of the roller bearing (case 3), there is a clear deviation (higher value) when the result of Equation (11) is compared with the results of Equations (12–13), the source of this difference is unknown, but it is suspected that it might come from the simplifications introduced by the approximated equations. However, the general methodology for the calculation of C remains valid in the present time when corrected with the bm factor. When it comes to the values given by the different companies, bearings of similar performance class and similar dimensions and static load rating were chosen when possible. It can be seen that there are some significant differences among them, and also, in some cases, with respect to the ISO values. Inspecting the values of the dynamic load ratings of Table 2, Company 2 seems to have applied larger technology factor bm than the ISO standard for all three cases that are examined.

For practicing engineers, the comparison shown in Table 2 is both self-explanatory and revealing. As discussed (Ref. 2), some bearing companies seem to deviate from ISO when it comes to such performance parameters as the dynamic load rating. In those cases, engineers are entitled to ask for explanations regarding the motivations that led to those deviations; as, for instance, different design, tolerances, material, and heat treatment and related confirmation of tests validating the change in load ratings. Even more important for engineers is to question the dynamic load ratings applied by recently established bearing companies which do not have endurance testing capabilities or facilities, yet quote in their catalogues the same (or higher) performance rating values as the ISO 281 standard.
Fatigue Load Limit
Another important rating parameter for bearing life is the fatigue load limit, Pu (or Cu in the ISO nomenclature). This parameter was formalized and introduced for practical bearing life rating in Ioannides et al. (Ref. 3). This development followed the initial consideration of the need of a fatigue limit (stress) for bearing life calculations presented in Ioannides and Harris (Ref. 8).
The standard ISO 281 (Ref. 1) defines the fatigue load limit Pu for a complete bearing as: “The bearing load under which the fatigue stress limit, σu, is just reached in the most heavily loaded raceway contact.” ISO 281 further specifies this limiting condition of the rolling contact as: “For rolling bearings of commonly used, high-quality material and good manufacturing quality, the fatigue stress limit is reached at a contact stress of approximately 1,500 MPa.”
For ball bearings, the contact stress can be accounted for by using Hertzian contact stress theory; thus the standard includes an analytical model for the calculation of the fatigue load limit of the bearing. In case of roller bearings, the presence of the roller profile requires the application of numerical schemes for the assessment of the maximum contact stress of the bearing; in general, a 3-D elastic contact solver is used. Given the fact that fatigue limit of the bearing material is standardized to a maximum contact pressure of 1,500 MPa (Ref. 1) for small bearings, it follows that the fatigue limit load of the bearing Pu is only a function of bearing internal geometry. Bearings from different manufacturers using similar, internal geometry and similar bearing steel material should have similar Pu.
The ISO standard (Ref. 1) adopts a definition for the fatigue limit stress of the bearing material that is expressed in term of maximum Hertzian pressure (1,500 MPa) of the rolling contacts of the bearing. The origins and validation of this value and possible variability are discussed in Gabelli et al. (Ref. 9). In addition to this basic fixed value, the standard (Appendix B) recognizes the need of a reduction of the fatigue load limit of the bearing according to increasing size. Starting with bearings that have mean diameter of 100 mm, for which the value of 1,500 MPa applies up to a penalization that varies with the rolling bearing diameter, following (100/𝒹m)0.5 and (100/𝒹m)0.3 for ball and roller bearings, respectively. This penalization of the fatigue load limit is introduced because bearings of large size may suffer from less manufacturing accuracy and less effective kneading of the ingots during the rolling and forging operations (Ref. 10). Reference 10 shows the details of this penalization in charts 28 and 29, where an asymptotic reduction of the fatigue limit load is indicated for a bearing mean diameter larger than 100 mm. In practice, some industries also apply specific fatigue limit reductions to increase safety, e.g. — aerospace.
General Methodology for the Calculation of Pu.
As mentioned earlier, a completely general methodology for the calculation of the fatigue load limit is pursued in this paper. In this way the calculation can be applied to ball and roller bearings alike — starting from the original basic definition of fatigue limit, as discussed in the previous section. The methodology has two main steps. The (i) pressure in the heaviest loaded contact is calculated and set to be equal to the fatigue limit of the standard, thus the general elastic contact problem needs to be solved to find which contact load gives the specified contact stress. And (ii), knowing the load of the heaviest-loaded contact, the corresponding bearing radial load giving rise to that contact load is calculated providing the fatigue load limit — Pu of the bearing.
General elastic contact solver. There are many numerical schemes to solve the general (3-D) elastic dry contact problem, but here the FFT methodology described in (Ref. 11) is used. Since this methodology is described in detail elsewhere, only a summary is included hereafter.
Following the description (Ref. 11) for a given pressure distribution on a half-space p(x,y), the surface elastic displacements u (x,y) can be calculated using Fast Fourier Transform (FFT) by applying the following equation.
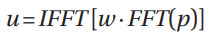
where w is a matrix containing numerical factors and is known as the frequency response function. For the elastic homogeneous problem, this matrix is calculated as follows:
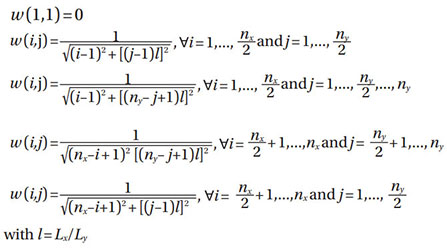
The contact problem is solved by finding the pressures that minimize the equivalent variational statement,
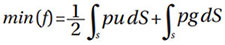
and
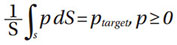
Where ƒ is the total complementary energy, g is the gap between the rigid plane, and the undeformed elastic surface.
Algorithm. The numerical algorithm employed to find the pressures from Equation (17) is also described in (Ref. 11). Beginning with a guess for the matrix that meets the equality and inequality constraints (a uniform pressure ptarget is usually chosen as start value of the iteration process), then —
- Calculate a candidate pressure matrix p' = p – grad [ƒ (p)]. In general, p' will violate the constraints grad[ƒ (p)] = u(p) + g for ƒ quadratic.
- Shift p' uniformly up or down so that the sum of the positive pressures equals the target load.
- Truncate all p' p' meets all constraints.
- Set p = p', and repeat until convergence.
Relationship bearing load — contact load. The relationship between the bearing load (radial) Er and the heaviest-loaded contact load is already given (Ref. 4); a consequence of this is Equations (10). Now, for most of the radial bearings the heaviest-loaded contact is often in the inner ring, but a check is always convenient to do. Therefore, from Equation (127) (Ref. 4):
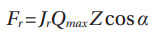
As described above, Ϳr = 0.2288 for a single-row ball bearing and Ϳr = 0.2453 for a single-row roller bearing, thus yields —
For ball bearings.
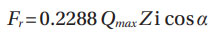
For roller bearings.
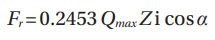
ISO methodology for the calculation of Pu.
Relationship bearing load — contact load. The relationship between the bearing load (radial) Er and the heaviest-loaded contact load is already given (Ref. 4); a consequence of this is Equations (10). Now, for most of the radial bearings the heaviest-loaded contact is often in the inner ring, but a check is always convenient to do. Therefore, from Equation (127) (Ref. 4):
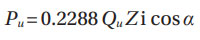
Where
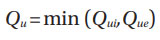
Ball bearings. Notice that the inner ring and Qui outer ring Que contact loads for a maximum pressure of σHu in the heaviest-loaded rolling element; they can also be calculated from Equations (8) and (9). However, here the equations given in (Ref. 1) are used.
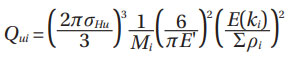
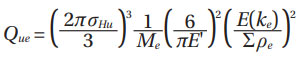
Where ∑ρ is the sum of curvatures (reciprocal or radii); E is the complete elliptical integral of the second kind, 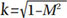 is the elliptical integral modulus; and M is the complementary modulus, M = a/b. Notice that Equations (22) require all the stress values (σHu, E') in N/mm2 and all distance values in mm.
is the elliptical integral modulus; and M is the complementary modulus, M = a/b. Notice that Equations (22) require all the stress values (σHu, E') in N/mm2 and all distance values in mm.
Roller bearings. For roller bearings, ISO recommends using a full numerical contact solver and does not provide an equation. However, based on Hertzian theory for line contact, an approximation can be derived for Qui and Que
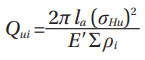
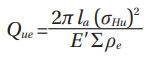
Finally,
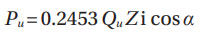
Where Qu is calculated with the use of Equations (21), (23a) and (23b). Notice that Equation (23) requires all the stress values (σHu, E') in N/mm2 and all distance values in mm.
Calculation examples of fatigue load limit. The same bearing examples given in Table 1 are used for the fatigue load limit calculation. Also, the catalogue values published by the same three different bearing manufacturers will be investigated. The methodology described in the previous sections is applied and the results are summarized in Table 3.

In the calculation for cases 1 and 2, the radii of the inner ring grooves are also required. This information is not available for the three selected bearing manufacturers, but based on ISO geometry values (Ref. 1), approximations can be used. Thus, for cases 1 and 2, ri ≈ 0.52Dw and re ≈ 0.53Dw.
For case 3, a straight roller profile with rounded chamfers is used in the calculation. For illustration purposes, the calculated results of case 3 (NU 408) are depicted (Fig. 1), where the contact pressure and sub-surface orthogonal shear stress τXZ are shown.
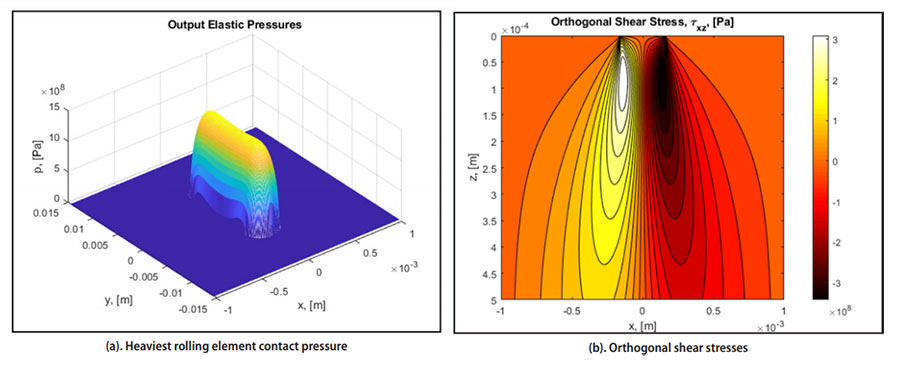
Notice that, for all the cases of Table 3, a somehow smaller limiting stress than the one given in ISO has been applied. The reason is that this stress has variability — as explained (Ref. 9). Initially, it is based on a value, max(τxz) = 360 ± 4% MPa, that corresponds to a maximum contact pressure of 1500 ± 4% MPa thus in order to be conservative in the calculation a minimum value of max(τxz) = 346 MPa was selected, which corresponds to a maximum contact pressure of 1,442 MPa. The maximum stress in Fig. 1(b) is max(τxz) = 349 ± 4% MPa, very close to 346 MPa.
Another observation from the results of Table 3 is that only open information for 2 of the 3 companies was found for Pu. It can be seen that Company 3 agrees somewhat well with the numerical and ISO methodologies, while Company 2 has substantially higher values. It is true that some companies have “higher-performance” bearings (reduced manufacturing tolerances, higher geometrical precision, improved surface finish, etc.) resulting in longer fatigue life which, in a way, could be considered as an increase of the value. But this would be non-conformal with ISO, since the value of the fatigue limit in ISO has been fixed and it is standardized to a mean of value of τxz = 1500 MPa with ± 4%.
Therefore the only feasible way to affect the fatigue performance of the bearing in a way that is consistent with the ISO requirements would be to use Equation (2) and modify the penalty factor ηa by redefining the value of the macro-scale stress factor . In this way it is clear that the fatigue limit of the bearing material is not affected by technological manufacturing improvements, and the progress in the bearing quality is indeed represented by rating factors that are designed expressly for that end. Load rating practices that simply increase the value of the fatigue load limit of the bearing Pu to reflect technological improvements are non-conformal with ISO 281. This may generate misperception in bearing users and distrust in the applied rating system as a whole. Thus these practices should be avoided.
Static Load Rating
The static load rating C0 is a performance parameter that does not enter directly in the rating life estimation of the bearing. However, it is a parameter related to maximum load bearing safety and its performance under low cycle fatigue. It is used in the estimation of the safety factor of the bearing regarding extreme loading conditions. Thus, it is important to discuss it here.
ISO:76:2006 (Ref.12) defines the static load rating as: “Experience shows that a total permanent deformation of 0.0001 of the rolling element diameter, at the center of the most heavily loaded rolling element/raceway contact, can be tolerated in most bearing applications without the subsequent bearing operation being impaired. The basic static load rating is, therefore, given a magnitude such that, approximately, this deformation occurs when the static equivalent load is equal to the load rating.”
And it goes on as indicated by the different nominal maximum contact pressures that can be used in practice for a quick determination of this rating:
“Tests in different countries indicate that a load of the magnitude in question can be considered to correspond to a calculated contact stress of
at the center of the most heavily loaded rolling element/raceway contact. The equations and factors for the calculation of the basic static load ratings are based on these contact stresses.”
Therefore, the numerical calculation of the static load rating follows a very similar process as the fatigue load limit, but using different stress levels when it comes to individual bearings. For standard static rating values, ISO 76 (Ref. 12) provides all the equations needed for the calculation of the static load rating — as shown below:
For ball bearings.
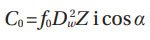
With the ƒ0 constants given in Table 1 of the ISO document (Ref. 12).
For roller bearings.
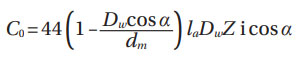
In the above equations, all units of length are in mm and calculated loads C0 are in N.
Calculation examples of static load rating. The same examples are considered. Table 4 shows the results and comparison with values given by the three main bearing manufacturers. It can be seen that in general there is good agreement between the calculated values and reported values from different manufacturers. The numerical method shows also minor deviations. Taking the ISO values as reference, the maximum deviation is of 5% observed for Company 2; but this is to be expected since the exact details of the bearing internal geometry are unknown and approximated here. This can introduce the observed variation.

For practicing engineers, the comparison of C0 values can be a good reference point when bearings of very similar internal geometry and material hardness are compared. It can be seen that there is more consistency among different bearing manufacturers with this load performance parameter than with any of the others.
Data Back-Up via Testing
Experienced rolling bearing companies should always be backing the values of rated performance of catalogue products using endurance testing. Of course, testing also has limitations, e.g.: (i) only certain bearing sizes make economic sense to test; (ii) tests are performed, mostly under stationary loading conditions; (iii) and tests can target only rolling contact fatigue — which is one of the main failure modes of rolling bearings. Nevertheless, despite these limitations, fatigue testing can provide strong statistical validation of the dynamic load ratings that are applied to bearings, particularly in the case where this methodology is systematically applied through the years so that data-pooling and trend analysis can be applied, providing an overview of the performance of the products over the years and across different types and sizes of the products.
Endurance testing is an important instrument to reduce the risk related to the improper application of standardized dynamic load ratings to lower-quality bearings. Such bearings are, in principle, outside the scope of the ISO 281 standard. However, given the imprecise formulation of the scope of the standard, this can be difficult to prove. The risk of an improper use of the standard is high — especially in the case of bearing products originated from new manufacturing companies that are not equipped with testing facilities for the verification of the dynamic rating of their products. Thus for new manufacturers, the application of ISO 281 offers a simple and ready-to-use solution for the performance rating of their products.
Many of these companies present their products as “fully ISO compliant” to impart a positive perception. While in reality, this description is not qualified to represent either the actual quality or actual dynamic performance.
In contrast, well-established bearing companies with a long tradition in bearing fatigue life ratings routinely perform endurance testing of their products to assess and verify the C values quoted in their catalogues. In the following, typical endurance testing methods used for the assessment of C dynamic load rating of rolling bearings are briefly reviewed. The fatigue limit (σHu) cannot be assessed via endurance testing due to the extremely long testing times it would require. However, other techniques can be applied — like ultrasound testing of steel (Ref. 2). For the static dynamic load rating C0 verification, static load testing in bearings and brinelling measurement can be applied.
Verifying the dynamic load rating C by testing. Bearing companies with experienced engineering generally apply best-in-class endurance testing practices (Refs. 13–14). Endurance test results are then evaluated using rigorous Weibull statistical analysis (Refs. 15–16). Such test methods are briefly summarized hereafter.
A common endurance-testing practice to verify the dynamic load rating C of a bearing is to conduct at least two full endurance tests on a randomly selected population of bearing samples. The tests are usually performed under good lubrication conditions (κ ≥ 2). This is done to remove any significant influence of the lubrication on the rolling contact fatigue life of the bearing that is measured.
The load and speed of the test are chosen to minimize the running time of the test. Typically the suspension time of test is set to be > L50 of the expected fatigue life under the given test condition. This ensures that a sufficient sample size of bearings failures are generated (≥ 6) during the test — thus allowing for good precision of the Weibull statistics results.
In practice, this often implies running a bearing sample population of about 20 or 30 bearings per each test under load conditions of 1 ≤ C/P ≤ 3, depending on bearing type and size. The test in this way will provide a good metrics of the life of the bearings and related confidence intervals of the results. This is particularly the case for Figure 2, i.e. — that several endurance test results are merged into a single test data pool.
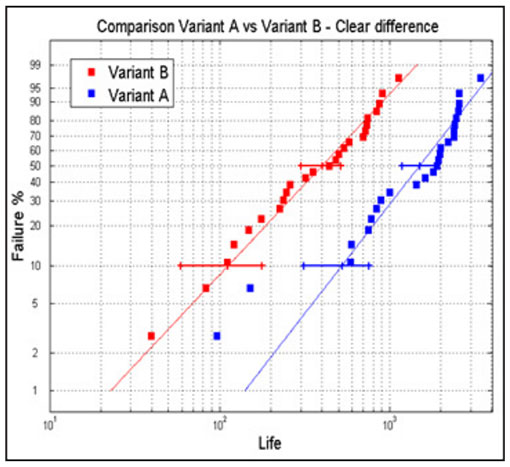
Figure 2 shows a typical example of Weibull plots from comparative endurance tests of two bearing populations (A) and (B). The results of the test show a clear difference in performance of the two bearing populations. This can be seen from the confidence intervals of L10 and L50 the life of the two test series that are clearly well apart from each other.

Reverse calculation of the bearing life, Equation (1), is used to estimate the value that will give a calculated life below the confidence interval of the measured L10 life. This is needed to ensure the strong experimental significance > 95% of the dynamic load rating that is verified, as schematically illustrated (Fig. 3).
This set-up of the model ensures that all calculations will result in predicted lives within the high percentile region of the experimental significance of the measured L10 life. On the contrary, if a model is set to coincide exactly on the measured L10(50%) this would imply a weak experimental significance. In other words there is a low probability that the endurance tests are able to verify the results of the calculated life. Indeed, in such a case about 50% of the times the calculated life could find itself at the right-hand side of the endurance tests’ Weibull line, thus overpredicting the fatigue life of the bearing.
As discussed earlier, the dynamic load rating C can be obtained from ISO 281 using the bearing’s overall geometry (Ref. 7), and the constant factor bm related to the technology and quality of manufacturing. In some cases, bearing companies use this factor to reflect some recently introduced technological improvements in manufacturing, e.g. — high-strength steel and heat treatment — which may surpass the ISO standard values. This is possible and should be acceptable when the new values are verified by proper endurance testing practices, as discussed above. Unfortunately, rolling bearing endurance life testing for the dynamic load ratings of rolling bearings is not part of the ISO standard. This might create some uncertainty in the procedures that are applied and in the dynamic load rating in use. This is also why the authors strongly favor the introduction of endurance testing standards for rolling bearings in the ISO.
Discussion
The process of calculating performance rating parameters (C,Pu,C0) in rolling bearings has been systematically reviewed in this paper. It can be seen that, in general, advanced numerical schemes fit well with the simplified ISO equations. In the comparison carried out with values reported by three well-established bearing manufacturers, it is found that the performance parameters that are affected by the largest variability are,C and Pu. To practicing engineers, this suggests C0 as a good reference parameter to compare the real internal geometry of bearings originated from different manufacturers. About this, particularly significant is the case of Pu, since this parameter is derived from the same numerical scheme used to calculate C0 (the only difference is the contact stress level that is applied); thus similar behaviors should be expected.
For example, if two companies have the same reported C0, they should also have the same and similar C (within a small variation of the application of the bm factor). Where this is not the case, engineers are entitled to question the validity of the values that are reported and to request clarification. In general, well-established bearing companies regularly perform endurance testing to verify the load ratings published in their catalogues. Typical endurance testing practices for the verification of the dynamic load ratings of rolling bearings are briefly reviewed in this paper. A sufficient number of bearings, i.e. — population sample — need to be endurance-tested to gather the necessary statistical data of the fatigue performance of the bearing. Equation (1) is then applied to calculate the L10 life, corresponding to a given C rating. For a positive verification of the dynamic load rating, the calculated life L10 should be located well on the left-hand side of the Weibull line to achieve a high degree of experimental significance. Therefore, it must always be: L10,calculated ≤ L10(95%), (Fig. 3). In addition to this type of experimental verification, practicing engineers can also check the quoted C value (Ref. 7) by simply manually measuring the bearing geometry and quantities used in Equations (12) and (13). After adjustment of the results using the corresponding ISO values for bm, the calculated C value should be a good approximation of the bearing manufacturer’s reported value.
Due to the continuous high demand for rolling bearings, many new bearing manufacturers are entering the market today. It is unlikely that these new players have adequate endurance testing capabilities for the verification of the dynamic load ratings that are quoted in their catalogue. Yet, the new manufacturers take direct advantage of the ISO 281 (Ref. 4) rating formulae that are valid only for: “commonly used, high-quality, hardened bearing steel in accordance with good manufacturing practices, the value of which varies with the bearing type and design.” Therefore the practicing engineer should question the validity of the dynamic load rating, particularly in the case of new bearing manufacturers that do not apply endurance testing methods for the verification of the load ratings of their products.
Finally, it is well known that in modern applications sub-surface failures are a rare occurrence. This is due to the good knowledge and experience accumulated over the years — certainly reflected in the work shown in References 3–5. All three of the discussed rating parameters refer to Hertzian stresses or subsurface condition of the bearing. When they do occur, most of the time an explanation related to overloading or material defects can be found (Ref. 17). However, most issues that rolling bearings face today are fatigue damage occurring at the very surface of the bearing raceway, where tribological fatigue mechanisms are playing a major role. Models to describe these issues involve mixed elastohydrodynamic lubrication (EHL) of the rolling contact (Refs. 18–21), and not just the Hertzian stress and general contact mechanics. The rolling contact fatigue of the raceway surface implies the combined effect of EHL lubrication, roughness, friction and wear. This is why the authors have developed a novel approach to bearing fatigue life prediction that separates the surface from the sub-surface survival of the bearing rolling contact (Refs. 22–23). Therefore, the reader should wonder if it is not the time to introduce more suitable dynamic load rating factors for rolling bearings, as has been suggested in the case of gears (Ref. 24).
Conclusions
Three main performance parameters used in rolling bearing application engineering have been methodically reviewed: the dynamic load rating C, the fatigue load limit Pu and the static load rating C0. The ISO equations for the calculation of these three parameters were also discussed, along with more general numerical calculation schemes. Calculated values using both procedures were compared. Published values of the corresponding performance parameters quoted from three well-established bearing companies were provided for reference, and as examples of present day rating practices. In the discussion, simple guidelines have been outlined to distinguish between likely and unlikely “truthful” and consistent values. Finally, from this analysis the following conclusions can be outlined:
- Numerical contact mechanics schemes and analytical ISO equations are in general agreement for all three parameters, C,Pu,C0.
- Reported performance parameters of three well-established bearing manufacturers show that, (unlike the value of Pu) the static load rating C0 represents the most consistent factor to compare the internal geometry and design variation among bearing manufacturers.
- Good work practices of bearing manufacturers must include systematic verification of their catalogue load rating, using well-established endurance testing methods. This is true also for the application of the ISO 281 load ratings or for the validation of rating change resulting from new technological developments.
- The lack of a quantitative definition of the bearing quality and quality practices in rolling bearings by ISO 281 and the undifferentiated application of this standard by newcomer bearing manufacturers with no testing facilities or practices to verify their ratings, call for the need of an ISO standard to describe best endurance testing practices and statistical data analysis for the rating of rolling bearings.
Acknowledgment. The authors want to thank Mr. Bernie van Leeuwen, SKF Research and Technology Development, for his kind permission to publish this paper.
References
- International Standard ISO 281, Rolling Bearings – Dynamic Load Ratings and Rating Life, 2nd Ed.; 2007.
- Gabelli, A., A. Doyer and G.E. Morales-Espejel. “The Modified Life Rating of Rolling Bearings — A Criterion for Gearbox Design and Reliability Optimization,” AGMA Technical Paper 14FTM16, pp. 1–16, 2016.
- Ioannides, E., G. Bergling and A. Gabelli. “An Analytical Formulation for the Life of Rolling Bearings,” Acta Polytechnica Scandinavica, Mechanical Engineering Series No. 137, The Finnish Academy of Technology, 1999.
- Lundberg, G. and A. Palmgren. “Dynamic Capacity of Rolling Bearings,” Acta Polytechnica Mechanical Engineering Series, Royal Swedish Academy of Engineering Sciences, vol. 1, No. 3, 7, pp. 1–50, 1947.
- Lundberg, G. and A. Palmgren. “Dynamic Capacity of Roller Bearings,” Acta Polytechnica Mechanical Engineering Series, Royal Swedish Academy of Engineering Sciences, vol. 2, No. 4, 96, pp. 1–33, 1952.
- ISO Technical Report ISO/TR 1281-1. Rolling Bearings – Explanatory Notes on ISO 281 – Part 1: Basic Dynamic Load Rating and Basic Rating Life, 2008.
- Parker, N., “Desktop Engineering — How to Calculate Dynamic and Static Load Ratings,” Power Transmission Engineering #2 (February), pp. 40-43, 2015.
- Ioannides, E. and T.A. Harris. “New Fatigue Life Model for Rolling Bearings,” Trans. ASME, J. Trib., 107, pp. 367–378, 1985.
- Gabelli, A., J. Lai, T. Lund, K. Rydén, I. Strandell and G.E. Morales-Espejel. “The Fatigue Limit of Bearing Steels – Part II: Characterization for Life Ratings Standards,” Int. J. of Fatigue, 38, pp. 169–180, 2012.
- ISO Technical Report ISO/TR 1281-2. Rolling Bearings – Explanatory Notes on ISO 281 – Part 2: Modified Rating Life Calculation, Based on a Systems Approach to Fatigue Stresses, 2008.
- Morales-Espejel, G.E., A.W. Wemekamp and A. Félix-Quiñonez. “Micro-Geometry Effects on the Sliding Friction Transition in Elastohydrodynamic Lubrication,” Proc of IMechE, Part J, Journal of Eng. Tribology, 224, pp. 621–637, 2010.
- International Standard ISO 76. Rolling Bearings – Static Load Ratings, 3nd ed.; 2006.
- Andersson, T. “Endurance testing in Theory,” Ball Bearing Journal 217, pp.14–23, 1983.
- Leenders, P. “Endurance Testing in Practice,” Ball Bearing Journal 217, pp. 24–31, 1983.
- McCool, J. I. “Evaluating Weibull Endurance Data by the Method of Maximum Likelihood,” ASLE Transactions, 13:3, pp. 189–202, 1970.
- McCool J.I. and R. Valori. “Evaluating the Validity of Rolling Contact Fatigue Test Results,” Tribology Transactions, 52:2, pp. 223–230, 2009.
- Manieri F., K. Stadler, G.E. Morales-Espejel and A. Kadiric. “The Origins of White Etching Cracks and their Significance to Rolling Bearing Failures,” International Journal of Fatigue, 120, pp.107–133, 2019.
- Morales-Espejel G.E., A. Gabelli and E. Ioannides. “Micro-Geometry Lubrication and Life Ratings in Rolling Bearings,” Proc. of IMechE, Part C, Journal of Mechanical Eng. Science, vol. 224, pp. 2610–2626, 2010.
- Morales-Espejel, G.E. and V. Brizmer. “Micropitting Modelling in Rolling–Sliding Contacts: Application to Rolling Bearings,” Trib. Trans., 54, pp. 625–643, 2011.
- Morales-Espejel, G.E., V. Brizmer and E. Piras. “Roughness Evolution in Mixed Lubrication Condition due to Mild Wear,” Proc. IMechE, Part J, J. of Mech. Eng., 229 (11), pp. 1330–1346, 2015.
- Brizmer, V., H.R. Pasaribu and G.E. Morales-Espejel. “Micropitting Performance of Oil Additives in Lubricated Rolling Contacts,” Trib. Trans., 56(5), pp. 739–748, 2013.
- Morales-Espejel, G.E., A. Gabelli and A.J.C. de Vries. “A Model for Rolling Bearing Life with Surface and Subsurface Survival—Tribological Effects,” Trib. Trans., 58(5), pp. 894–906, 2015.
- Gabelli, A. and G.E. Morales-Espejel. “A Model for Hybrid Bearing Life with Surface and Subsurface Survival,” Wear, 422–423, pp. 223–234, 2019.
- 24.Morales-Espejel, G.E. and A. Gabelli. “A Model for Gear Life with Surface and Subsurface Survival: Tribological Effects,” Wear, 404–405, pp. 133–142, 2018.
Appendix A — Detailed Parameter Description, Dynamic Load Rating
The use of Equations 4–7 requires the definition of the following quantities:
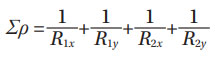
In equation (A1) the radii are negative for concave curvatures.
The amplitude of the normalized orthogonal shear stress τxz /ρ0 is given by:
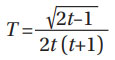
Where t can be obtained by solving the following equation:
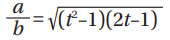
The position of the maximum shear stress is determined by,
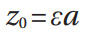
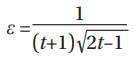
Finally, from Equation (101) of (Ref. 4):
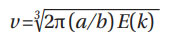
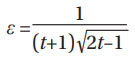
Now, the exponents are defined as follows (Ref. 4):
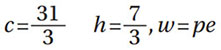
For point contact (ball bearing): 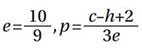
For line contact (roller bearings): 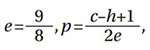
exponent e corrected from 3/2 to 9/8 (Ref. 5).