Integrated Hybrid Servo Motors vs. Standard Integrated Servo Motors
Integrated Hybrid Servo Motors vs. Standard Integrated Servo Motors: How Do They Stack Up?
Different motor types favor different application areas. No single style has advantages in all application spaces. Direct drive applications favor hybrid servos while high-speed, geared down applications tend to favor the conventional servo motors. Misapplication of a conventional servo into a direct drive application may result in just one-third of the expected efficiency and provide only 40% of the continuous power at a typical application speed. This leads to 160% to 450% more heat being dissipated by the conventional integrated servo motor, as compared to a similarly sized NEMA 23-frame (4 inches long) integrated hybrid servo motor.
Integrated servo motors fall into a couple of main camps, i.e. — traditional low-pole-count AC brushless, and hybrid servo, which use high-pole-count AC brushless motors. The latter may also be used open-loop as step motors. The integrated hybrid servo motors — as used in this comparison — are operated as true servo motors using vector drives. These comparisons do not hold for step-loss, prevention mode step motor drives — even though the same style of motor may be in use. This closed-loop vs. open-loop performance difference is also true of low-pole-count motors in that a given motor generally performs significantly better when using a full servo control than when that same motor is operated open loop using a variable speed drive.
Fundamental Motor Differences
Hybrid servo motors are based on high-pole-count (typically 100-pole) motors — typically called “step motors” in open-loop operation. Traditional servo motors normally use lower-pole-count (typically 4-16-pole) motors. Given the other motor factors being the same, the torque constant (Nm/A) for a motor increases with the number of poles, and the speed goes down by the same ratio. The torque constant (if losses are accounted separately) equals the voltage constant when expressed as volts/radian/sec. In this example comparison, “A” brand integrated servo motor lists the voltage constant as 6.6v/1,000 rpm, which corresponds to .06 v/radian/sec, thus equaling .06 Nm/A, and a winding resistance of 1.1 ohm. The QCI integrated hybrid servo has a measured voltage constant of .227 v/radian/sec, and a winding resistance of .66 ohms. This means that this conventional servo requires more than 3.5 times as much current to produce the same torque at the shaft as does the hybrid servo. Power loss is calculated in the copper windings by Ploss equals I2R. This corresponds to more than 20 times the power dissipated, just to hold the same torque when the motors are stopped. Thus a high-torque constant is very beneficial at low to medium speeds; however, the high torque constant also causes a higher motor back-EMF for a given speed, which reduces the voltage available to the drive current into the motor at higher speeds. This condition limits the top speed of the motor. These differences make the hybrid servo motor very useful for many direct drive applications, but limits their use in very high-speed applications, where the lower-pole-count motor wins out.
Comparing Torque Curves
The torque curves are shown (Fig. 1) for the two motor types. As you can see, the hybrid servo has more continuous torque — up to approximately 2,000 rpm — and more continuous torque than the “A” motor has peak torque — up until approximately 1,500 rpm. These are important speeds for direct drive applications, i.e. — with the motor directly driving the load without a gearhead. A typical lead screw, i.e. — quarter-inch, 24-inches-long, both ends secured with a single bearing — has a critical speed approximately 1,600 rpm, while extending the leadscrew to 36 inches drops the critical speed to just over 700 rpm. A typical direct drive belt drive (1" diameter pulley = 3.14"/revolution) moves at 52-inches-per-second while rotating at 1,000 rpm.

Output Power Available
Figure 2 shows that the hybrid servo has approximately constant power from 700 rpm up to nearly 1,500 rpm, which again nicely covers the direct drive requirements. This means that the speed can be chosen within this speed range and will still be fully utilizing the motor capabilities. The conventional servo data shows power out through 7,000 rpm, but has been truncated to fit the graph. While the continuous power of the “A” motor does extend up to 226W at higher speeds, the continuous power at 1,000 rpm is just 35W compared to 90W for the QCI-X23C-3 hybrid servo. Therefore, determining the preferred motor type definitely depends upon how the motor is being applied!


Motor Efficiency vs. Speed
The motor efficiency for the QCI hybrid servo was directly measured (Fig. 2), while the efficiency for the traditional servo was approximated, based on the torque and the I2R losses and estimated speed-related losses, as well as the input current of 6.6A at 48v producing .33Nm at 6,500 rpm (226W out, 318W in, some 92W waste heat). With the continuous torque curve stated as based on an 85C case temperature, the power being dissipated by the motor has been taken as approximately continuous across the speed range for these calculations. What is readily apparent is that the hybrid servo motor and controller are significantly more efficient than the conventional servo motor — up to about 3,200 rpm. At 1,000 rpm, mid-range for many direct drive applications, the hybrid servo is some 225% as efficient than the continuous operation of the conventional servo motor, and some 300% as efficient when comparing against the peak torque curve of the conventional low-pole-count motor (which is still only producing about 64% of the hybrid servo torque). Again, there is a wide speed range of high-efficiency operation for the hybrid servo motor. Note: the curve has been somewhat truncated to show the direct drive range of speeds; the “A” system eventually reaches an efficiency of 71% at the nominal continuous power point of 6,500 rpm. While this may be useful for applications that actually need this speed, it is not accessible for most direct drive applications.
Although both motor types have an efficiency of zero at zero speed, the hybrid servo system takes only some 20W to hold a 1.2 Nm load when stopped, compared to an estimated 90W needed to hold the conventional servo at .31 Nm, and an estimated 250W for the peak holding torque of .56Nm when stopped! This difference is very important in gluing fixtures, grippers, vertical loads, clamps, and similar loads which spend a significant portion of their time stopped with torque present.
Typical Direct Drive Applications
Many direct drive applications require motor speed between 250 rpm to 2,000 rpm; for example, piston direct displacement pumps for precision delivery are usually in the 250 to 500 rpm range. Belt drives, as shown earlier, are 200-1,000 rpm. Lead screws typically range from 500 to 1,500 rpm for a wide range of applications, but the speed is not only limited by the critical speed (first resonance) of the lead screw, but also by the lead nut speed rating, which can often limit the speed of even short lead screws.
So How Are These Hybrid Servos Less Expensive?

The motors used for the hybrid servos are based on the step motors — produced at a rate of many millions of motors per month. The designs use a significantly smaller amount of magnetic materials, and the usually single magnet (with a long 3-stack motor having 3 magnets) is axially aligned with the rotor, making for easy installation that does not require careful alignment and grinding. Although the pole count is high, the single magnet is shared between all of the rotor poles by a clever homopolar design. These motors are also internal permanent magnet motors (IPMs), which is a technology just starting to be used for higher-end servos and high-efficiency motors. The use of the IPM design allows for field-weakening methods to be used that allow the peak power and efficiency speed ranges to be extended. The field-weakening methods also allow the ultimate motor speed — albeit at a reduced torque — to be extended beyond that which would normally stall the motor due to the back EMF exceeding the drive voltage. Due to the higher pole count, the commutation frequency for these motors is significantly higher than for the low-pole-count motors, but the speed increase in digital signal processors (DSPs) has made this less of a problem.
Summary
The high continuous torque provided by the high-pole-count motor allows the motor to actually reach its maximum power capability in many direct drive applications without needing a gear head to match the motor speed to the application speed. This means you can actually use the rated power at the needed speed. Using a higher-speed-rated motor in a typical direct drive application means buying a 200W motor and driver and then only being able to get 30W or 40W into your application, or adding a gearhead, which — with its added size and cost and reduced reliability — really changes the comparison! As shown, proper matching of the motor speed characteristics to the load requirements significantly reduces power usage and the resulting wasted heat. This result may be counterintuitive when considering a traditional servo is thought to have high efficiency, but this high efficiency is only available in the narrow range near its optimal operating speed, i.e. — the efficiency is much lower when operating below that speed. Also remember — for positioning applications, the holding power requirements may actually dominate the total heating!
The hybrid servo motor very effectively services a sizable range of direct drive applications — with lower cost, smaller size, and a higher efficiency than is accessible with conventional servo motors. (Acknowledgements: The author wishes to thank the QuickSilver Controls Engineering department for providing the various photos and performance plots used in this article.)
For more information
Donald Labriola, P.E.
QuickSilver Controls, Inc.
990 N. Amelia
San Dimas, CA 91773
Phone: (909) 599-6291
 Donald P. Labriola II, president and founder of QuickSilver Controls, Inc., specializes in servo controllers and motors, with a special focus on cost-effective motion control. He has been granted eleven U.S. patents as well as numerous international patents. His background includes over 40 years of motion control, including 20 years in medical instrument design. Labriola enjoys gardening, camping and Ham radio — and motion control!
Donald P. Labriola II, president and founder of QuickSilver Controls, Inc., specializes in servo controllers and motors, with a special focus on cost-effective motion control. He has been granted eleven U.S. patents as well as numerous international patents. His background includes over 40 years of motion control, including 20 years in medical instrument design. Labriola enjoys gardening, camping and Ham radio — and motion control!Why Pole-Count Matters: Magnetic Gearing
For a given rotor diameter, the number of magnetic poles on the rotor directly affects the torque available, the top speed available, and the power needed to hold a load. Higher pole counts lead to higher torque, lower top speed, and a higher motor quality factor:
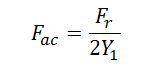
The effect is as if a hypothetical gearhead had been inserted — and is called “magnetic gearing” in the literature.
How it works. For the same rotor dimensions and gap flux, for a given speed, the rate of change of gap flux varies directly with the number of poles, as the frequency of the variation varies directly with the number of poles. Given the same winding window, for a given drive current rating, the number of turns is almost constant (although some designs do allow for a slightly larger fill factor, thus a few more turns). The result is that the back-EMF * drive current increases approximately linearly with the number of poles. As the back-EMF constant in V/radian/sec equals the torque constant in Nm/A, the continuous torque thus increases with the number of poles. In Figure 4, the higher rate of change of flux with angle is apparent for the higher pole count rotor — even though the magnitude of flux for both motors is equal. For a given number of turns on the stator pole, the back-EMF generated is:

V = –N × ∂Φ/∂t (number of turns times the rate of change of flux with time)
Tradeoff: Although the increase in torque is helpful, the increase back-EMF reduces the speed needed to generate enough voltage to oppose a given power supply level. Thus the higher torque capability must be traded against the maximum speed for a given power supply voltage.
The back-EMF constant of the motor in volts/radian/sec is numerically equal to the torque constant in Newton*meter/amp if the motor moving losses are separately accounted. For the same winding configuration, doubling the back-EMF doubles the torque constant, and only requires that half of the current hold the same load. With the resistive losses being P = I2R, doubling the torque constant only requires only one fourth of the power to hold a given torque load. Tripling the torque constant brings the power needed to that same load down to 1⁄9 the power — all else being the same.
Thus, low-speed high-torque applications can be effectively handled without a gearhead by increasing the pole count of the motor. The high pole count motor is effectively “magnetically geared” down. One size does NOT fit all: selecting the appropriate motor for the application can optimize the performance and minimize the price.
Similarly, very high-speed, low-torque applications are best handled with lower-pole-count motors to keep from having excessive back-EMF, which would otherwise exceed a given power supply voltage.