Low Noise and Transmission Error Epicyclic Gearbox Designs

T. J. Lisle, B. A. Shaw, R. C. Frazer, Y. Yang, L. Zhao

Introduction

Minimizing gear transmission error (TE) and the resulting noise and dynamic load is a subject well researched and understood. Quite simply, changes in tooth load sharing, mesh stiffness, deflections and geometric deviations from the true involute, introduce small oscillatory rotations of the wheel relative to the pinion. Common TE optimization approaches aim to minimize the change in load distribution amongst the teeth, whether by increasing the transverse contact ratio, as is common in high contact ratio (HCR) spur gears, or by introducing an axial overlap ratio by adopting helical gears. Indeed, a superior helical solution maintains an integer overlap ratio (IOR) such that the theoretical load line lengths remain constant, regardless of the transverse contact ratio. Irrespective of the chosen macro geometry, gears are also exposed to loaded deflections and random manufacturing errors, which further influence the operational transmission error which is often minimized via micro geometry corrections.

With regards to epicyclic gearboxes, whether it be a planetary, star or solar design, there exists another unique feature which can be manipulated to further minimize TE — the phasing of the planets — for which, previous research has shown to have a significant impact on the dynamic characteristics of the gearbox (Refs. 1-10).

An epicyclic gearbox designed such that all the planets enter mesh with the sun at the same time, and all the planets enter mesh with the ring at the same time, is often said to be in-phase or factorizing. This condition is achieved if the number of teeth on the sun, divided by the number of planets establishes an integer value. Alternatively, the system may be designed such that the planets enter and exit mesh at different phases, which is said to be out-of-phase, non-factorizing or sequential. This can be achieved while still maintaining equal planet spacing, and since the individual engagements are staggered, the total transmission error can be significantly reduced. It is for this reason that a sequential design is believed to be superior for minimizing torsional vibrations and TE, albeit at the expense of possible transverse and rotational vibrations.

Regardless of whether a design is sequential or not, there also exists the phasing between the sun/planet (S/P) to the planet/ring (P/R), which can themselves be either in or out of phase.

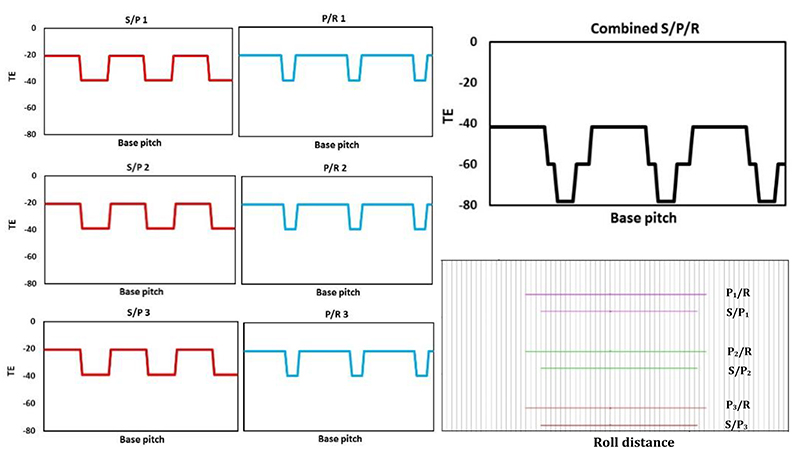
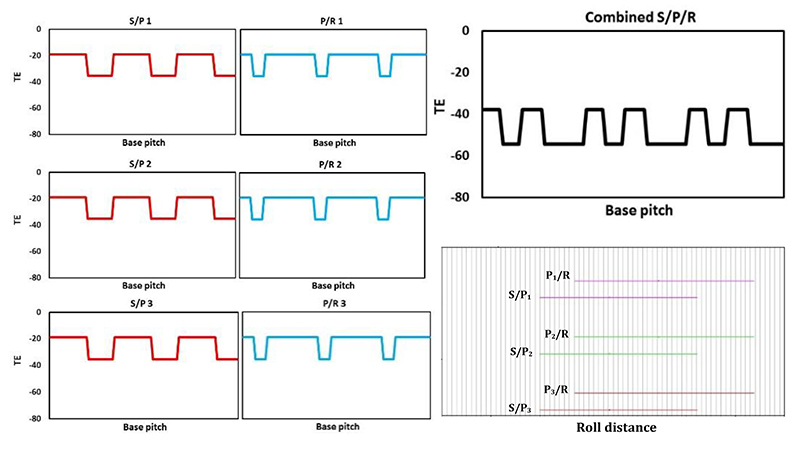
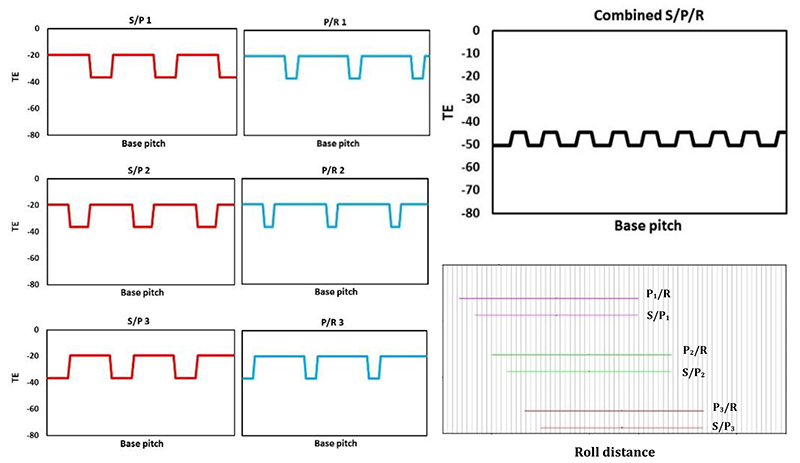
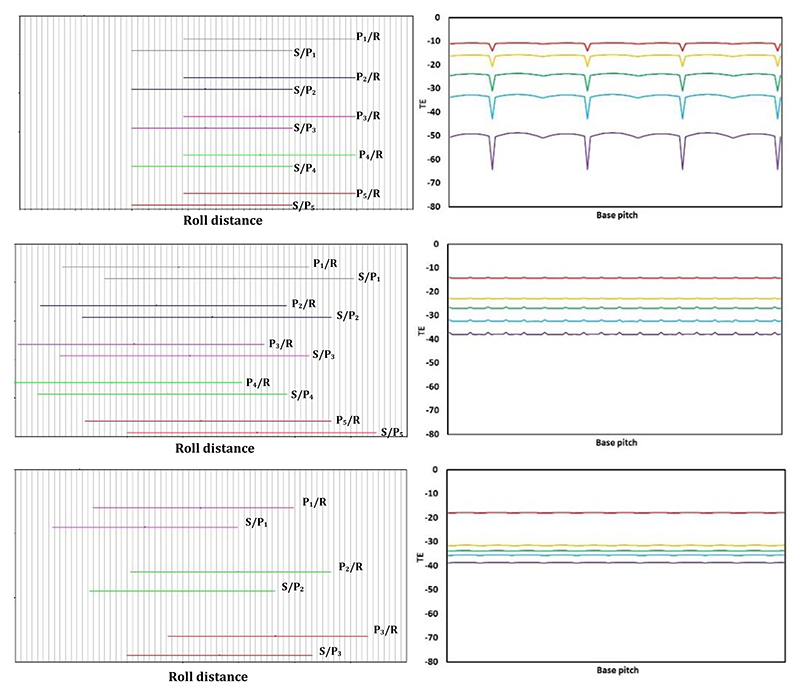
The notion of phasing is investigated using commercially available gear analysis software (Dontyne) (Ref. 11) which adopts simple strip theory (Ref. 12) to establish the quasi-static TE. Here, tooth stiffness is assumed parabolic and a maximum at the pitch point, falling to approximately 70% at the start and end of active profile (Ref. 13). Combined with load sharing, micro geometry corrections and misalignments, the total expected quasi-static TE can thus be established. Using an iterative approach, the analysis also accounts for unequal load sharing amongst the planets due to differences in the instantaneous mesh stiffness between out-of-phase planets. An arbitrary example illustrating the effects of phasing is presented in Figures 1 through 3, for factorizing and non-factorizing designs, with ‘n’ planets, and sun, planet and ring tooth numbers of zs, zp and zr respectively. For simplicity, each planet experiences equal load with a constant mesh stiffness, the details of which are presented in Table 1. Here, without presenting the specific details of load or geometry, the magnitude of the TE is irrelevant, and the example is merely presented to provide the reader with a greater understanding of planetary phasing, and the potential reduction in TE with only slight modifications to tooth numbers.

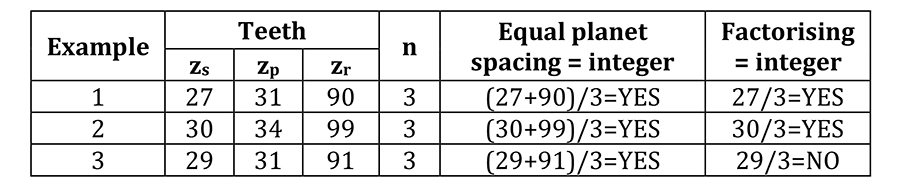
Example 1 is factorizing, such that the phasing of all S/P are identical. Likewise, the phasing of all P/R are identical, as illustrated in Figure 1. Note however, regardless of the factorization, the length of the path of contact of the S/P is less than that of the P/R, as illustrated in the phasing diagram Figure 1, whereby the P/R engage and exit mesh before and after the S/P respectively. In this example, the total combined TE is a direct combination of the S/P and P/R. Example 2 is still factorizing, however there is a distinct shift in the phasing of the S/P with that of the P/R as illustrated in Figure 2. As a consequence, when the TE of the S/P is combined with that of the P/R, the total TE (17 μm) is significantly less than that presented in example 1 (37 μm). Finally, example 3 adopts a non-factorizing design such that the phasing of all the S/P are different, as are the P/R. As a consequence, the total TE has been reduced to only 6 μm, as illustrated in Figure 3.

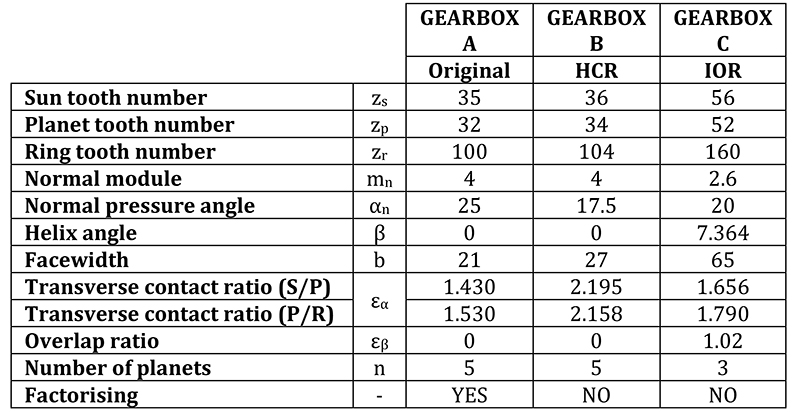
Macro Geometry Design

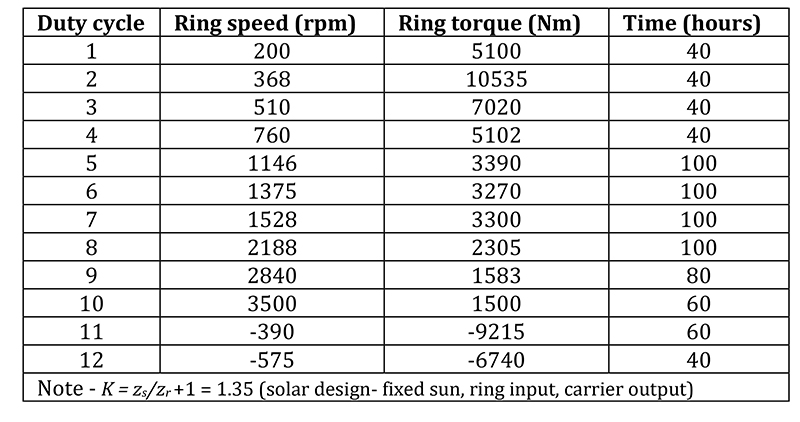
The objective of this research was to utilize the theory of phasing to optimize an existing epicyclic gearbox to produce the lowest TE, whilst understanding the resulting implications with regards to the complexity, cost, weight and possible risks. To facilitate this, an initial design and detailed specification was required, whereby a load spectrum, together with a required ratio and epicyclic arrangement fully defined the system, as detailed in Table 2. Each design was analyzed in the first instance for strength, in accordance with ISO 6336:2006, then optimized by analyzing the elastic mesh deflections such that the transmission error was further minimized using micro geometry corrections. In addition to the optimization process, each gearbox was fully designed and detailed, including housings, carriers, shafts, bearings, splines and the lubrication delivery system, only after which can the true benefits and implications of each design be fully understood.

Gearbox A. The base design was an existing spur gear system with 5 planets, and sun, planet and ring tooth numbers of z_s = 35 z_p = 32 and z_r = 100 respectively, such that the planets were equally spaced and factorizing.

Gearbox B. With only slight modifications to the tooth numbers specified in Gearbox A, and a small change in the gear ratio, the macro geometry was modified such that it was now non-factorizing by adopting sun, planet and ring tooth numbers of z_s = 36 z_p = 34 and z_r = 104 respectively, while maintaining equal planet spacing and the use of 5 planets. The basic rack profile and pressure angles were modified such that a transverse contact ratio greater than 2 was achieved, resulting in an HCR design.

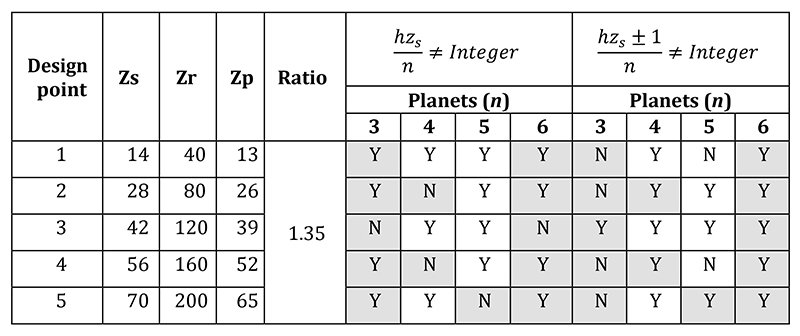
Gearbox C. Gearbox C adopted helical gears, with an integer overlap ratio slightly larger than 1. Table 3 presents a list of viable tooth numbers, without addendum modification, which satisfied the required gear ratio, equal planet spacing, and the potential to eliminate torsional and transverse modes of excitation, based on equations 1 and 2 respectively, analogous to that previously presented by Palmer and Fuehrer (Ref. 2), for the first harmonic (h). Equal planet spacing is represented by the shaded cells in Table 3.

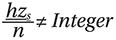
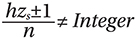
Taking into consideration cost, weight, planet load sharing factors, shaft sizing and bearing loads, design point 4, with 3 planets, was considered a good compromise based on gear diameter and module and gave a balanced design with regards to contact and bending safety factors. Furthermore, it provided a sequential design with equal planet spacing, albeit at the expense of potential transverse vibrations. The final macro gear geometry chosen for all three gearboxes, A, B and C, is presented in Table 4. Detailed gear stress analysis for both new designs (B and C) was conducted in accordance with ISO 6336:2006, using the load spectrum presented in Table 2, ensuring each proposed design provided minimum contact and bending fatigue safety factors of 1.0 and 1.4 respectively. Each design adopts a suitable planet load sharing factor determined in accordance with AGMA 6123-B06, depending on planet numbers and system flexibility. The remaining mechanical design of both Gearbox B and C was conducted in accordance with 1) AGMA 6001-E08 for shaft stressing, 2) ISO 281 2007 for advanced bearing life, 3) DIN 5480:2006 for spline geometry, and 4) SAE M-117 for spline stress analysis, the results of which are illustrated in Figure 4 and 5.

Micro Geometry Design

The macro geometry established for the HCR gearbox (B) and IOR gearbox (C) largely defined the likely magnitude of expected TE of the system. However, loaded deflections and random manufacturing errors will exacerbate the true operational TE, and must be further minimized with suitable micro-geometry corrections. This requires a detailed understanding of the likely gear misalignments expected during operation. Including the loaded and no-load (manufacturing) errors in both the transverse plane (profile) and across the facewidth (helix slope) of the gear. It is obvious therefore, that gears can only be truly optimized at a single load, and any deviations from which will change TE, stress and power loss. To optimize the gears in gearbox B and C, an input torque of 3000 Nm was chosen, at 1500rpm, as this torque level was common throughout the load spectrum.

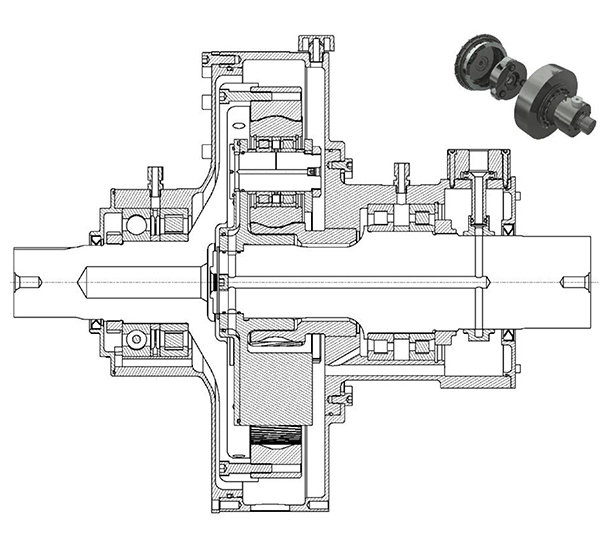
Loaded helix slope deviation (f_sh). The loaded shaft deflections, including both bending and torsion, were established for the sun, planet carrier and ring, using ANSYS finite element analysis (FEA) whereby the actual component architecture was analyzed under operational loads and boundary conditions. The ring and sun gear were analyzed by incorporating the base tangent and axial forces where applicable, located at the point of planetary contact, thus establishing the resulting deflection in the direction of the line of action, across the face width of the gear. The planet carrier pins were subjected to twice the tangential force (2F_t) and an overturning moment (F_a/d_p) to compensate for the axial gear forces, where applicable. An example analysis of gearbox C is illustrated in Figures 6 through 8.

Loaded Profile Slope deviation (δ). In the transverse plane, each tooth deflects by an amount (δ) which is proportional to the mean mesh stiffness (C_γ), facewidth (b) and transverse load (F_t). This deflection value is used as a first approximation for the amount of tip relief required in the optimization process.

Manufacturing helix slope deviation (ƒ_ma).

In addition to loaded deflections, it is necessary to establish the likely random manufacturing helix slope error (ƒ_Hβ) of the gears (based on the gear quality grade), the shafts and housing (ƒ_ca) to establish an overall maximum expected manufacturing helix misalignment (ƒ_ma).

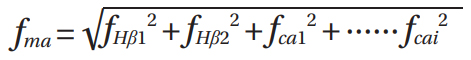
Consequently, the loaded shaft deflections (ƒ_sh) and manufacturing errors (ƒ_ma) can be summed and halved to provide the amount of crowning (C_β) required for the optimization analysis.

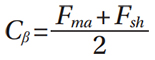
Manufacturing profile slope deviation (f_α).

The manufacturing profile slope accuracy (f_α) which is obtained directly from the gear quality grade provides an indication of the design sensitivity to manufacturing quality. That is, if the magnitude of the profile tolerance is large compared the mean mesh deflection and tip relief, it may have a significant impact on the transmission error.

Results

Once the loaded and random manufacturing errors were established, the system was accurately optimized. Tip relief was chosen to be linear starting at the highest point of double (HCR) and single (IOR) tooth contact which often provides the lowest noise designs, but at the expense of higher contact stresses. A five-step approach was undertaken to further optimize the gears, as follows.

1. Evaluate the gear performance with no misalignments or micro-geometry corrections. This will provide baseline results.
2. Starting with the minimum estimated tip relief established in accordance with equation 3, systematically increase the tip relief until non-conjugate contact is eliminated, without the start of contact occurring unnecessarily far away from the tip.
3. Using the minimum required amount of tip relief established in step 1, introduce helix slope errors equal to f_ma+ f_sh. This provides baseline results for the gears without crowning.
4. Introduce an amount of crowning established in accordance with equation 5, together with tip relief.
5. Check the sensitivity of the design under possible profile slope errors of f_α.

With the optimized macro and micro geometry, the TE was established for all three gearboxes, the results for which are presented in Figure 9, at various torques up to 10k Nm at 2k Nm intervals.

Discussion and Conclusions

Gearbox A was a simple factorizing spur design, with 5 planets. This base design, without any micro geometry modifications, exhibited significant TE as illustrated in Figure 9. With only slight amendments to the tooth numbers, pressure angles and tooth height, a non- factorizing HCR gearbox was designed which significantly reduced the TE. With the introduction of the IOR Gearbox, also non-factorizing, this was reduced even further to sub-micron levels across the entire load spectrum. Hence, the use of phasing, combined with increasing the transverse or axial contact ratio has been shown to dramatically reduce TE. However, every design concept had significant ramifications, as follows.

1. Choosing a factorizing design such that the torsional mode of excitation is neutralized at meshing frequency, does not eliminate torsional excitation at certain higher harmonics or other transverse and rotational excitations.
2. The HCR design is vastly simplified, mainly due to the lack of axial gear forces. Conversely, the IOR design required a much larger gear face width to a) accommodate suitable planet bearings, and b) reduce the magnitude of the helix angle required to maintain an IOR, and therefore reduce the axial forces, and planetary moments.
3. The HCR gearbox adopted a simple side spray lubrication system via jets situated at various static positions around the housing. This minimizes churning loses, improves efficiency, and was deemed suitable to lubricate the gears and single planet bearings. However, concern lay with the IOR gearbox, and the need to ensure adequate lubrication to both planet roller bearings — specifically that closest to the carrier — which may not receive satisfactory splash lubrication. Thus the IOR gearbox adopted a more complex delivery system, via the carrier shaft, simultaneously providing oil to the planet bearings, via the pin, and the planet gears, via the carrier walls. Here, the oil jets are static in relation to the planet positions, such that they can supply a constant jet of oil directly into and out of mesh, with a jet velocity equal to or greater than the pitch line velocity. However, this required a non-contact rotating union delivery system, accurately constrained via a complex two-bar linkage system. See Figure 5 for further details.
4. Sequentially phased designs produce a small residual radial load. However, that said, even an in-phase design, with balanced radial loads and therefore a theoretical requirement for no radial support, may still exhibit a potentially much greater residual radial load due to unequal planet load sharing. As a consequence of this load, and any potential external radial loads generated due to the eccentricity of any connecting shafts into and out of the gearbox, both the input (ring) and output (carrier shafts), in these examples, were fully supported.
5. IOR axial forces must be reacted by, and accounted for, in the life of suitable ring shaft bearing. Note that since the sun gear was static, the axial loads were easily reacted, whilst those on the planet carrier cancelled.
6. The added complexity of adopting helical gears, with the need for twice as many planet bearings, large facewidth gears and a complex lubrication system, produced a design which was considerably heavier than the HCR design. It may therefore be assumed that HCR design is a sensible compromise, however, it should also be noted that the sensitivity of the HCR TE due to pitch and profile deviations were such that a greater gear accuracy would be required to maintain the benefits of such a system.
7. The benefits of phasing is more complex than simply ensuring a design factorizes or not. The phasing diagrams presented throughout, highlight the need to consider the relative positions and length of engagement of the sun/planets, planet/ring and ring to sun.
8. Finally, the entire design process is incredibly iterative, and very difficult to publish in a logical fashion. However, it is only once the entire process is complete, together with the corresponding detailed designs, can one fully understand the true implications of any concept design choices.

References

1. Seager, DL. “Conditions for the neutralization of excitation by the teeth in epicyclic gearing,” Journal of Mechanical Engineering Science. 1975; 17(5):293-299.
2. Palmer, WE and RR. Fuehrer. “Noise control in planetary transmissions,” In: 28th Annual earthmoving industry conference; 1977: SAE Technical Paper.
3. Hidaka, T, Y. Terauchi and K. Nagamura. “Dynamic behavior of planetary gear (6th report, influence of meshing-phase),” Bulletin of the JSME 1979; 22(169):1026-1033.
4. August, R, R.Kasuba, JL Frater and A. Pintz. “Dynamics of planetary gear trains,” NASA Contractor report 3793. 1984.
5. Kahraman A. “Planetary gear train dynamics,” Journal of Mechanical Design. 1994; 116(3):713-720.
6. Kahraman A, Blankenship GW. Planet mesh phasing in epicyclic gear sets. International Gearing Conference; Newcastle upon Tyne, September 1994.
7. Parker RG. A physical explanation for the effectiveness of planet phasing to suppress planetary gear vibration. Journal of sound and vibration. 2000; 236(4):561-573.
8. Parker RG, Lin J. Mesh phasing relationships in planetary and epicyclic gears. Journal of Mechanical Design. 2004; 126(2):365-370.
9. Ambarisha VK, Parker RG. Suppression of planet mode response in planetary gear dynamics through mesh phasing. Journal of Vibration and Acoustics. 2006; 128(2):133- 142.
10. Boguski B, Kahraman A. An experimental study on the motion transmission error of planetary gear sets. ASME Power Transmission and Gearing Conference; 23rd Reliability, Stress Analysis, and Failure Prevention Conference, Boston Massachusetts, USA, 2-5 August 2015.
11. Palmer D, Fish M. Gear production suite planetary load analysis module, 2015.
12. Palmer D, Fish M. Evaluation of methods for calculating effects of tip relief on transmission error, noise and stress in loaded spur gears. American Gear Manufacturers Association fall technical meeting; 2010.
13. Munro RG, Palmer D, Morrish L. An experimental method to measure gear tooth stiffness throughout and beyond the path of contact. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. 2001; 215(7):793-803.