Analysis of the Operational Behavior of a High-Speed Planetary Gear Stage for Electric Heavy-Duty Trucks in Multi-Body Simulation
Analysis of the Operational Behavior of a HighSpeed Planetary Gear Stage for Electric HeavyDuty Trucks in Multi-Body Simulation
Introduction
More restrictive environmental requirements are prompting vehicle manufacturers to develop electrically powered mobility solutions. In the field of commercial vehicles, distribution transport is of great interest due to its impact on the environment in urban areas. Within the research project “Concept ELV2,” an integrated drive unit consisting of an electric machine and gearbox for heavy-duty distribution traffic is being developed and tested. The sub-project “Concept ELV2 Technology Development,” which is being carried out in cooperation with the Daimler AG, the Institute for Automotive Engineering at RWTH Aachen University (ika) and the Institute of Electrical Machines at RWTH Aachen University (IEM), includes the development of an innovative and efficient e-axle at RWTH Aachen University. Due to the high rotational speed of electric machines compared to usually used diesel engines, the transmission topology changes significantly. With a high power density combined with a high transmission ratio, planetary gearboxes are increasingly being used in these applications.
With the trend towards electrically driven vehicles, the reduction of driving resistances and thus optimization of power density is of great interest due to the limited energy density of batteries. However, increasing power density usually results in higher load-related displacements in the transmission systems. Simulation methods should be used to evaluate the influence of structural stiffness on operational behavior since test bench investigations are time and cost-intensive. Especially in the case of automotive and commercial vehicle transmissions, interactions between the transmission stages should be taken into account, and, if possible, overall transmission systems should be simulated. The objective of this report is the analysis of the influence of a planet pin position error on the operational behavior under consideration of different simulation model configurations in MBS. Therefore an FE-based method will be developed and a verification with other simulation methods will be performed.
Multi-dimensional Excitation Effects in Planetary Gear Stages
In contrast to single or multi-stage cylindrical gearboxes, the dynamic misalignment behavior of planetary gear stages is more significant due to the kinematic coupling between the tooth meshes and the power flow split. A planetary gearbox with three planets already shows a static overdetermination for non-flexible gear components (Ref. 1). In addition to the number of planets, there are other factors that influence the dynamic operational behavior of planetary gearboxes. A division of the influences on the operational behavior into three main groups is shown in Figure 1. A distinction is made between geometrical constraints, manufacturing deviations, and system stiffness. The geometrical constraints include, in addition to the number of planets, the mesh sequence of the planets, which has an effect on the temporal sequence of the meshing stiffness. In contrast to planetary gearboxes with spur gears, the helix angle of helical gears leads to excitations by the opposite axial forces of the sun-planet and the planet-ring gear mesh (Ref. 2).
To evaluate the operational behavior of planetary gearboxes, it is very important to consider the system stiffness. The load-related deformations of the components, such as the planet carrier, cause a multi-dimensional misalignment of the gears in the tooth contact (Figure 1). In particular, the interaction with additional gear stages and thus forces acting externally on the planetary gearbox can have effects in form of load-related displacements (Ref. 3). This occurs especially with power density optimized gearboxes. The static overdetermination of a planetary gearbox can be reduced with movable components. Then the stiffness of the bearings in addition to the mass inertia of the movable component must be considered in the simulation. The effects described in Figure 1 are examples since interactions and overlapping of those effects can occur.
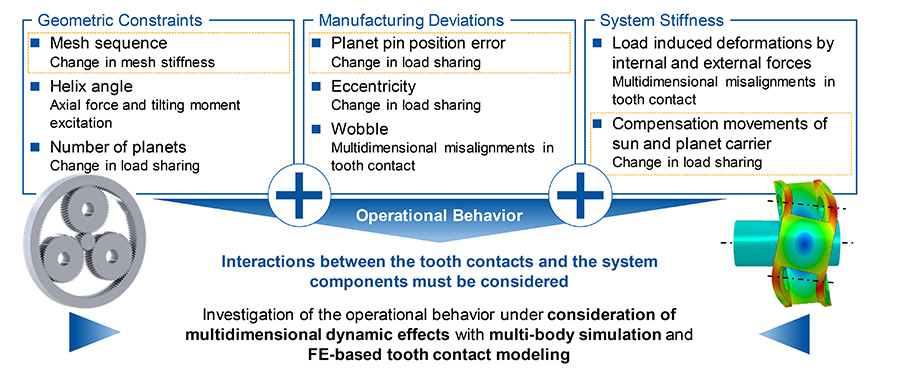
Manufacturing deviations are a main influencing variable in the excitation of gears. In case of planetary gearboxes this effect is intensified due to the kinematic overdetermination. The torque sharing between the planets is particularly influenced by planet pin position errors and eccentricity at the sun or planet gear. Similar to cylindrical gears, manufacturing deviations in form of wobble can also have a significant negative influence on the operational behavior. In addition for planetary gearboxes, a wobble of the planet carrier must be taken into account.
Extensive research contributions exist for the static and dynamic calculation of the torque sharing in planetary gearboxes, whereby mostly a plane modeling approach without three-dimensional displacements of the gears is used. If the effects of manufacturing deviations and stiffness influences on the operational behavior of planetary gearboxes are investigated, simplified models are often used to calculate the tooth stiffness or the contact areas are calculated with analytical methods (Refs. 2, 4–7).
An overall system modeling approach including the local stiffness changes in the tooth contacts due to the misalignment of the gears and system components with a focus on the influence of manufacturing deviations is not possible with simplified models. The FE-based calculation of the mesh stiffness considering the misalignment in the tooth contacts in the dynamic multi-body simulation (MBS) offers the possibility to simulate the interactions between the tooth contacts and the system components (Ref. 8).
Modally reduced FE-models can be integrated for the stiffness-appropriate modeling of the components so that entire transmission systems can be simulated. In this report a method for the simulation of planetary gearboxes in dynamic multi-body simulation is presented. For this purpose, a verification of the simulation results with quasi-static methods will be carried out in the following chapter.
Verification of the Developed Tooth Contact Calculation in MBS
To verify the tooth contact calculation GEARFORCE6D developed by the authors, a comparison with validated programs is performed. For this purpose, simulations with FE-STIRNRADKETTE V4.2.24, ZAKO3D V2.10, and ABAQUS CAE are carried out (Refs. 9-10). The FE-STIRNRADKETTE determines the contact line based on an analytical approach. In contrast, the contact area is numerically calculated in ZAKO3D, ABAQUS, and the method presented here. To reduce the numerical effort, the new method approximates the contact area by a contact line, while ZAKO3D and ABAQUS use the entire contact area.
To evaluate the differences, calculations of the load-related transmission error and the total transmission error are performed with different point-grid resolutions of the tooth flanks. The general FE software ABAQUS CAE is used as a reference for the total transmission error due to the general contact calculation approach. The sun-planet mesh of a planetary gearbox is used as a gear set example. In addition to the basic gear data, the calculated transmission errors of the various simulation methods for a pinion torque of T1 = 66.7 Nm are shown in Figure 2. In the upper diagram on the right side in Figure 2, the load-related transmission error is shown over one pitch. The higher frequency deviations of the results of ZAKO3D are smaller in their amplitude at the finer resolution of 41x41 points than at the coarser resolution.
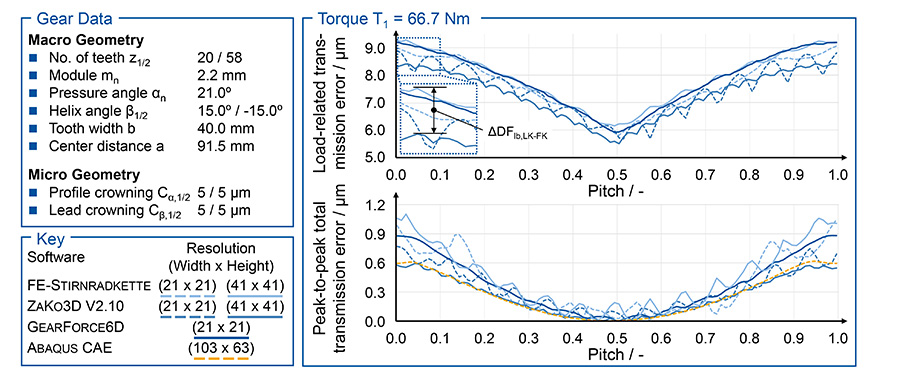
For the FE-STIRNRADKETTE, there are also differences in the results when using different flank resolutions. At a resolution of 21x21 points, deviations can be seen that are caused by the 20-node hexahedral elements of the FE-model. The lower stiffness of the nodes on the element edges compared to the nodes of the vertices has an effect on the resulting overall stiffness curve in the form of deviations. This stiffness variation becomes visible in the load-related transmission error. At a resolution of 41×41 points the deviations of the results of the FE-STIRNRADKETTE are reduced. In comparison, the deviations of the results of GEARFORCE6D are already small even at a resolution of 21×21 points. This is due to the 8-node hexahedral elements of the used FE-model, which are also used in ZAKO3D and ABAQUS. With this FE element type there are no nodes on the edges, so that eight 8-node FE elements are used instead of one 20-node FE element. A disadvantage of the 8-node FE elements is the longer calculation time due to the higher number of elements.
There is a difference between the methods with a line-based and surface-based contact approach. The load-related transmission errors of the FE-STIRNRADKETTE and GEARFORCE6D show a variable offset of up to ΔDFlb,LK-FK = 0.8 μm in comparison to ZAKO3D with fine point grid and surface contact approach.
In the lower diagram of Figure 2, the fluctuation of the peak-to-peak total transmission error is shown for the different simulation approaches. First the high correlation between the results of ZAKO3D with fine resolution and ABAQUS is visible. In addition, a division of the methods according to contact approach is possible, so the results with a line-based contact approach (FE-STIRNRADKETTE and GEARFORCE6D) are above those with surface contact approach (ZAKO3D and ABAQUS). A possible explanation is an increase in the stiffness of the tooth contact by including several contact points in the profile direction when using a surface contact approach. Additional contact points are simulated in the mathematical spring model by additional springs, which increase the overall stiffness in a parallel connection. The variations in the results of the FE-STIRNRADKETTE depend on the chosen element types. The results of GEARFORCE6D show the smallest higher frequency fluctuations in addition to the results of ABAQUS. Due to the line-based contact approach, the results are higher than of those with a surface contact approach (ABAQUS and ZAKO3D).
Thus, the newly developed contact calculation of GEARFORCE6D represents a numerically efficient method for calculating the stiffness of tooth contacts. Especially for dynamic multi-body simulation, the reduction of periodic deviations is of great importance, as these otherwise cause an incorrect, numerically caused excitation in the entire system.
For the verification of the pressure calculation, simulations with the FE-STIRNRADKETTE, ZAKO3D, and ABAQUS were carried out and evaluated. The pressure distribution on the tooth flank for one pitch is shown in Figure 3 on the right. The results of ZAKO3D with a fine flank point-grid resolution (41×41 points) and ABAQUS show a high correlation. With a resolution of 21×21 points in ZAKO3D, the calculated pressures are up to 30% lower compared to the other methods. This is also evident when comparing the pressure curve in the middle of the tooth width, see Figure 3 top left. The pressure distributions of the FE- STIRNRADKETTE and GEARFORCE6D show both qualitative and quantitative similarities. The slight differences between the results of the line-based methods (FE-STIRNRADKETTE and GEARFORCE6D) and the area-based methods (ABAQUS and ZAKO3D) are due to the contact calculation method itself.
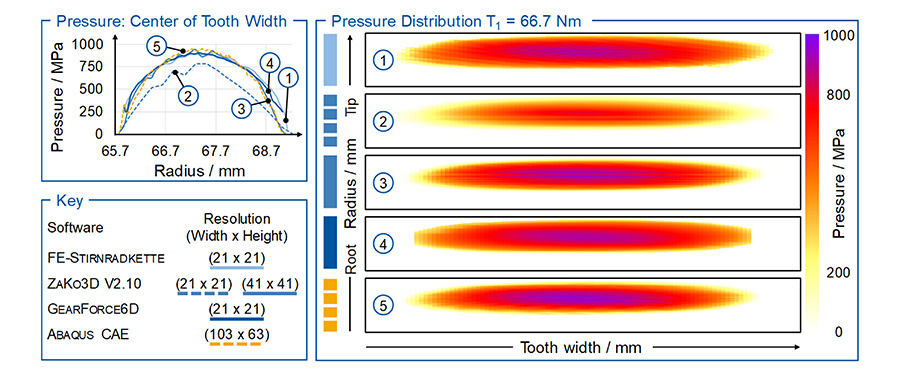
In summary, it can be stated that GEARFORCE6D allows the calculation of the transmission error and the tooth flank pressure with a high accuracy. Compared to the other simulation methods, the results show a high correlation. The number of points required to describe the numerical contact was in comparison always the lowest with an equal quality of results. In contrast to analytical contact methods used in the FE-STIRNRADKETTE, which also provide good results with a low flank resolution, GEARFORCE6D allows the consideration of displacements of the gears in the numerical contact model.
Effect of Manufacturing Deviations on the Operational Behavior of Planetary Gearboxes
Deviations from the ideal geometry occur in almost all manufacturing processes. They can usually only be reduced to a minimum at uneconomically high costs. Thus the possibility of a simulative evaluation of the effects of the deviations on the overall system behavior is even more necessary. In this chapter a multi-body simulation (MBS) model of the gear stages of an electrically driven rear axle for trucks in DASSAULT SYSTEMS SIMPACK 2019X is built up. The developed method GEARFORCE6D is used for multi-dimensional simulation of misaligned tooth contacts in the dynamic MBS. In the subsequent analysis, a manufacturing deviation on the planet carrier is varied and the operational behavior is analyzed. Here the designed planetary gearbox is in the focus and is extended in the last section by a helical gear stage, the final drive.
Introduction of the Test Gear Set and the Model Configuration. The gear data of the designed planetary gear set is shown in Figure 4. The gearbox topology is shown next to it. The planetary gearbox is used in a two-shaft operation with a fixed ring gear. Starting from an electrical machine with a maximum power of PEM,max = 235 kW, and a maximum speed of nEM,max = 10,000 rpm, the power is transmitted via the sun and the three planets of the planetary gearbox to the planet carrier. From there the power is transmitted via a helical gear stage to the differential cage and thus to the axle. The electrical machine, the gear housing, the differential, and the axle are not part of the simulation model but could be simulated in further investigations.
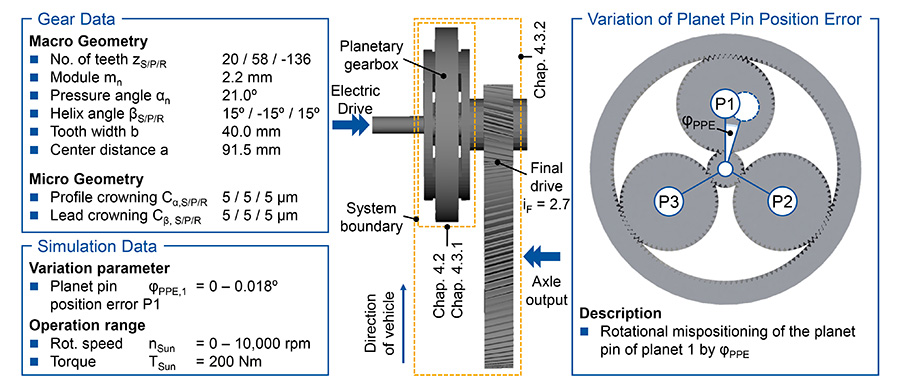
The planet pins are modeled as pinion shafts and are supported on both sides in the planet carrier. The planet carrier is supported by bearings on the input and output side in the reference coordinate system.
For the sun shaft, a fixed/floating bearing concept was selected. The radial stiffness of the floating bearing, which is located closer to the sun gear, is varied in the simulations. For the bearing stiffnesses empirical values were used, since the bearing selection was not yet carried out in the development process. To simulate the stiffness of the components, the sun shaft, the planet carrier, and the planet pins are integrated as modally reduced FE-bodies created with ABAQUS.
The simulated operating conditions are selected in the power range of the electrical machine. To analyze the dynamic operational behavior, a speed run-up of nSun = 0–10,000 rpm is simulated at a constant torque of TSun = 200 Nm, see Figure 4 bottom left. The electric motor can provide this torque over the entire speed range. This report focuses on the influence of a planet pin position error on the operational behavior. A planet pin position error describes a rotational mispositioning of the planet pin of the first planet. The position of the planet pin is thus rotated by the angle φPPE, see Figure 4 right. In the following sections, the planet pin position error is varied for different gearbox configurations from φPPE,1 = 0° to φPPE,1 = 0.018°. In addition, the radial bearing stiffness of the floating bearing of the sun shaft is varied so that the effects can be described for a stiff (cRadial,Sun = 400 kN/mm) and a flexible (cRadial,Sun = 4 kN/mm) sun shaft bearing.
In the analysis of the simulation results, the torque sharing between the planet gears in the sun-planet mesh is evaluated. For this purpose, the torque sharing factor TSFP (Torque Sharing Factor) is calculated for each planet p for each time step of the speed run-up according to (Ref. 1) and shown as maximum, average, and minimum value. In addition, the radius of the sun shaft trajectory and the dynamic radius variation around the mean radius are evaluated. Furthermore, the resulting misalignment and the occurring maximum Hertzian pressure in the sun-planet mesh is examined. Finally, the first tooth mesh order of the transmission errors between sun and planets and between sun and carrier is analyzed.
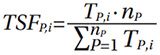
Where
TSF is the torque sharing factor
TP,i is the torque at planet p at time step i
nP is the number of planets
Influence of Mesh Sequence. The phase shift actually resulting from the number of teeth and assembly position causes a sequential mesh sequence. But first a symmetrical mesh sequence is simulated to compare the influence of different mesh sequences. For this theoretical application, the initial rolling positions of the gear meshes are synchronized in the simulation. The simulation model in this and the following subchapter includes only the planetary gearbox, thus interactions with the helical gear stage are neglected.
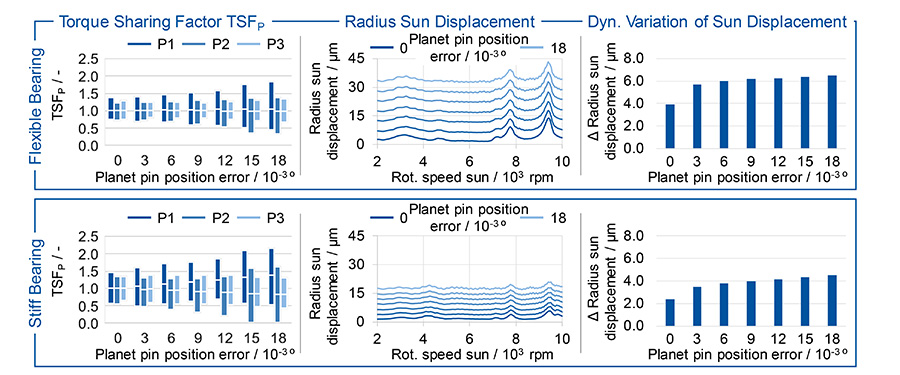
Symmetrical Mesh Sequence. The simulation results for the planet pin position error variation of Planet 1 and symmetrical mesh sequence are shown in Figure 5 and Figure 6. In the case of a flexible sun shaft bearing, the influence of the planet pin position error on the mean torque sharing is only slightly visible, see Figure 5 top left. Planet 1, which is affected by the planet pin position error of φPPE,1 = 0.018°, transmits in average 4.5% more torque with a mean torque sharing factor of TSF1,mean = 1.045 than with an ideal torque sharing. However, the fluctuation range of the torque sharing factors increases significantly up to TSF1,max = 1.277 at maximum planet pin position error. With a stiffer sun shaft bearing, the average torque sharing factor at the first planet is TSF1,mean = 1.375 and the maximum torque sharing factor is TSF1,max = 1.519 in the case of the highest planet pin position error, see Figure 5 bottom left.
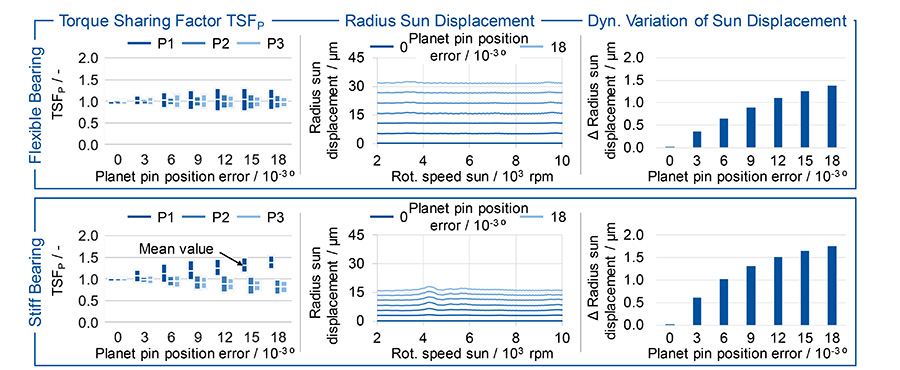
The explanation for the higher torque sharing factors can be found in the comparison of the radial sun displacement, see Figure 5 middle. For an ideal planet pin position, the sun remains in its radial starting position, as expected. In the case of a planet pin position error, the sun shaft performs a circular motion with the rotational speed of the carrier to compensate the deviation. If the planet pin position error is φPPE,1 = 0.009°, a radial deflection with a radius of the sun’s movement takes place in case of the flexible bearing of rdyn,sun,flex ≈ 15.5 μm, whereas a stiff bearing only permits a compensatory movement of up to rdyn,sun,stiff ≈ 7 μm. The lower adjustment movement of the sun shaft leads to higher kinematic constraining forces in case of the stiff bearing, which increases the transmitted torque by the protruding planet 1. The dynamic variation of the radial sun displacement over one revolution of the carrier shows smaller differences between the bearing stiffnesses, see Figure 5 right. The dynamic variation of the sun displacement also increases with an increasing planet pin position error.
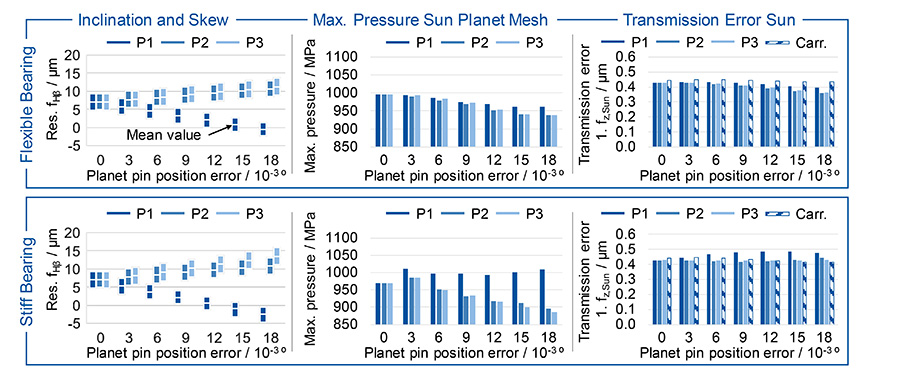
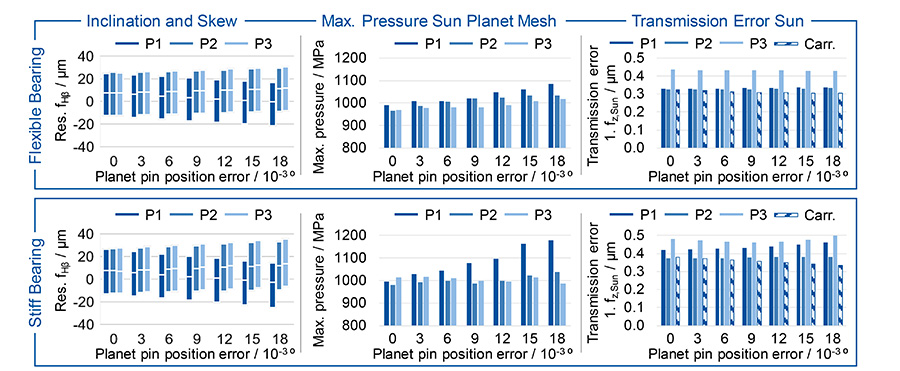
The sun shaft does not perform a purely translatory movement in its compensatory movement. Due to the bearings a tilting movement is superimposed. Thus, influences on the rotational misalignment in the tooth contact of the sun-planet-mesh can be expected. In Figure 6, the misalignment components inclination and skew in the tooth contact are converted into a resulting lead angle deviation ƒHβ according to Wittke (Ref. 11). They are shown on the left as bar plot with the minimum, average, and maximum.
Without planet pin position error, all planetary gears have a misalignment in tooth contact of ƒHβ = 7.0 μm. This depends on the tilting moment on the planet gears caused by axial forces and the load-dependent deformation of the carrier. The bar height in Figure 6 on the left represents the dynamic range of the misalignment. With increasing planet pin position error, the misalignment of the individual planets differs significantly. In the contact of the first planet, which is under higher load, the misalignment components inclination and skew compensate each other with a larger planet pin position error, independent of the stiffness of the sun shaft bearing. Since the amount of the sun displacement is different for the flexible and the stiff sun shaft bearings, the compensation also results from a displacement of the planet. Thus it can be concluded that an unbalanced torque sharing leads to a more optimal displacement of the system for the highest loaded planet. Since the mean values of the resulting displacement are less influenced by the stiffness of the sun shaft bearing, higher forces have to be applied to achieve the displacement with a stiff sun shaft bearing. That is the reason for the higher torque sharing factor in Figure 5 and the higher maximum tooth flank pressure in Figure 6. The lower transmitted torque in the two planets without planet pin position error leads accordingly to a maximum tooth flank pressure that is up to 12.4% lower. Here the differences between planet 2 and planet 3 are due to dynamic effects that become visible when evaluating the maximum value.
The first tooth mesh order of the transmission error of the first sun-planet mesh shows a nearly constant excitation in case of a soft sun shaft bearing, whereas the excitation at the second and third planet decreases. In contrast, the excitation with a stiff sun shaft bearing is higher at planet 1 and is constant for the other planets. The transmission error excitation of the first tooth mesh order between the sun and the carrier, which is shown by the dashed shape, is not significantly affected in both cases of bearing stiffness.
In summary, it can be stated that a planet pin position error leads to a significant negative effect on the dynamic torque sharing for a planetary gear-set with symmetrical mesh sequence. A more flexible sun shaft bearing offers the possibility of reducing the maximum torque sharing factors, which has positive effects on the maximum tooth flank pressure and the excitation behavior of sun-planet meshes.
Sequential Mesh Sequence. The simulation results with sequential mesh sequence are shown in Figure 7 and Figure 8. The average torque sharing factor is comparable to the results with a symmetrical mesh sequence. The dynamic fluctuation range of the load sharing factors is higher even without the planet pin position error. This is due to the time shift of the mesh stiffness in the sun-planet meshes because of the mesh sequence. With increasing planet pin position error the fluctuation range of the load sharing factors increases. With a planet pin position error of φPPE,1 = 0.018°, the load sharing factor of the first planet is TSF1,max = 1.364 for the flexible sun shaft bearing and TSF1,max = 1.724 for the stiff sun shaft bearing. The load applied to the tooth contact and surrounding components with a stiff sun shaft bearing is therefore up to 61.7% higher than without planet pin position error.
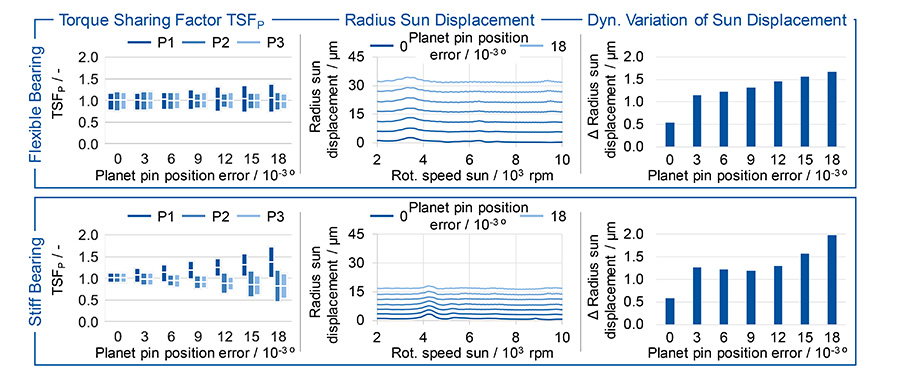
The radius of the sun displacement shows a low dynamic influence, which could not yet be determined with the symmetrical mesh sequence. Especially for small planet pin position errors, an increase of the dynamic radius variation can be seen, Figure 7 middle. Overall, the displacement movements of the sun gear are comparable with those of the symmetrical mesh sequence.
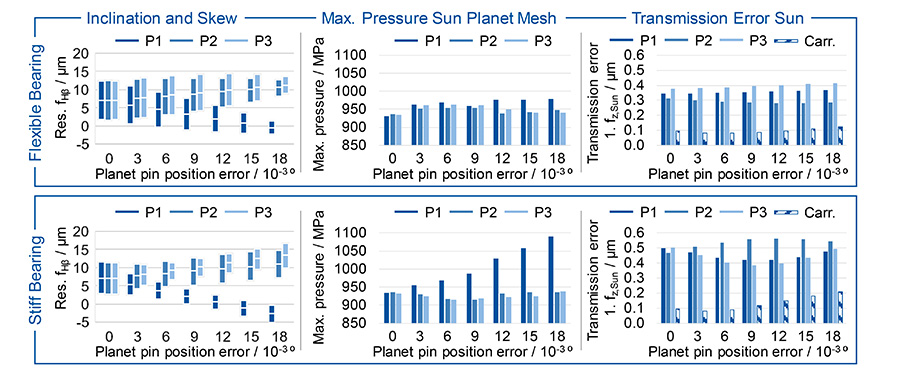
The misalignment in tooth contact is significantly higher than with symmetrical mesh sequence even without planet pin position error, see Figure 8. Due to the time-shifted tooth meshing and tooth forces, the planet carrier moves more, which results in higher misalignments in the tooth contact. This influence decreases with increasing planet pin position error. The planet pin position error is then responsible for the carrier movement and a compensating movement due to the mesh sequence is less significant. The fluctuation range of the misalignment in the tooth contact decreases with increasing planet pin position error. In general, the dynamic range of variation of the misalignment is smaller with a stiffer sun shaft bearing.
The effects of the planet pin position error on the tooth flank pressure are different for the sequential mesh sequence than for the symmetrical mesh sequence. In the sequential mesh sequence, the maximum pressure also increases with increasing planet pin position error in case of a flexible sun shaft bearing. The increase is less significant compared to the rigid sun shaft bearing. With a planet pin position error of φPPE,1 = 0.018°, and a stiff sun shaft bearing the maximum tooth flank pressure in the contact of the first planet is 11.2% higher than with a flexible sun shaft bearing. Compared to a symmetrical mesh sequence, a stiff sun shaft bearing leads to an increase of 7.9% in flank pressure.
While the load distribution, the misalignment in tooth contact, and the tooth flank pressure are negatively influenced by the sequential mesh sequence, the effects on the first order of the transmission error between the sun and the planet carrier are positive. Due to the time-shifted mesh stiffness of the individual sun-planet meshes, a more uniform overall stiffness between the sun and the planet carrier results.
Influence of External Loads and Misalignments
The modeling of the planet carrier without external forces of the following helical gear stage is a simplification. For this reason, in the next modeling step a load-related displacement of the carrier is applied by displacing the output-side bearing position of the planet carrier in the direction of the radial force of the helical gear stage by Δx = 10 μm. Thus the effects and interactions of an additional misalignment of the planet carrier can be analyzed and evaluated in a differentiated way. Afterwards the helical gear stage is included in the simulation model instead of the static misalignment of the carrier.
Tilted Planet Carrier. The results with a misaligned planet carrier are shown in Figure 9 and Figure 10 with an otherwise unchanged simulation model. The mean torque sharing factor TSFP,mean is not influenced by the misaligned planet carrier, see Figure 9 top left. Compared to the results without a misaligned planet carrier, it can be seen that the dynamic torque sharing with a stiff sun shaft bearing is subject to higher fluctuations, see Figure 7 and Figure 9. The radial sun displacement shows a continuous increase of the radius with increasing planet pin position error. With a flexible sun shaft bearing and a planet pin position error of φPPE,1 = 0.018°, the mean radius of the sun shaft trajectory is rdyn,Sun,soft ≈ 31.8 μm, whereas with a stiff bearing it is only rdyn,Sun,stiff ≈ 16.8 μm. The center of the circular trajectory of the sun is moved due to the displacement of the carrier but remains almost completely in one position during the speed run-up.
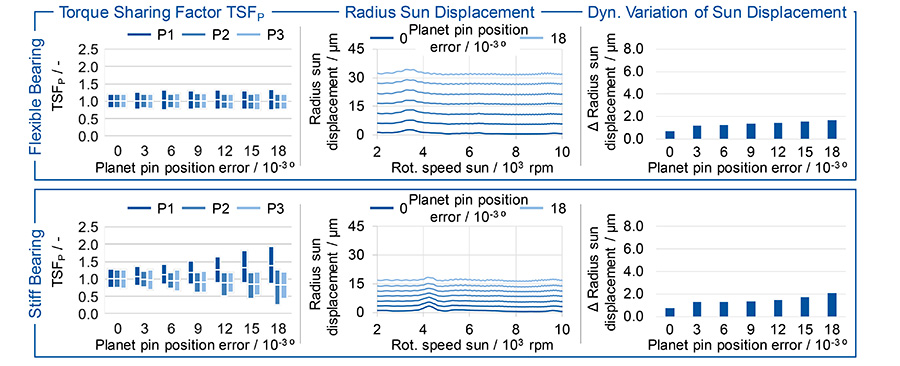
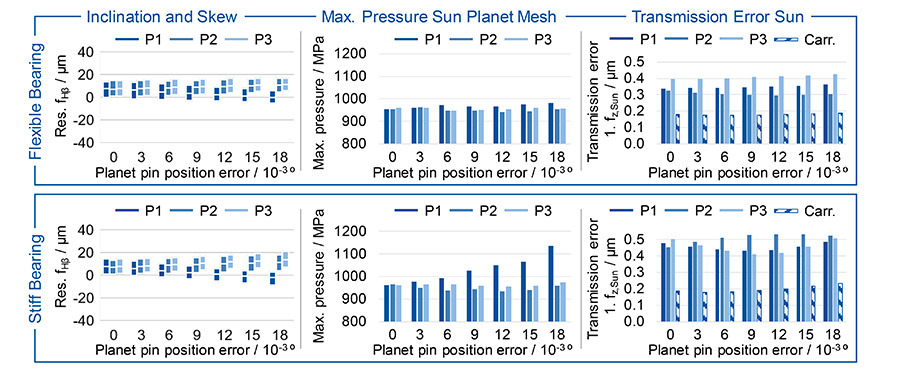
The displacement of the bearing position of the planet carrier causes a tilting of the planet carrier and the planet gears inside it. During one revolution of the carrier, each planet performs a wobble due to this misalignment. This multi-dimensional movement becomes visible in the variation of the resulting lead angle deviation ƒHβ in the sun-planet meshes, see Figure 10 left. Here, the mean value of the lead angle deviation in the results without carrier misalignment is comparable to those with carrier misalignment, so that only the range of fluctuation due to the wobble increases. The lead angle deviation oscillates with the first rotational order of the planet carrier around the respective mean value, whereby higher frequency oscillations from the interaction of the tooth mesh with the system are superimposed. The maximum tooth flank pressure is also influenced by the higher misalignment in the tooth contacts. It increases by 4.2% at the maximum planet pin position error and a stiff sun shaft bearing on the affected planet compared to the simulation with an ideal carrier position. The results show that a flexible sun shaft bearing can almost compensate the effects of a planet pin position error on the tooth flank pressure, see Figure 10.
The evaluation of the transmission error shows an increase in the excitation between sun and planet carrier for all simulation points compared to the results with an ideal positioned carrier. Especially with a small planet pin position error of φSTF,1 = 0.003°, the effect of the planet carrier misalignment with an increase in excitation of up to 125% in case of a stiff sun shaft bearing is significantly high. For larger planet pin position errors, the additional influence of the carrier displacement is lower, see Figure 10 right.
In summary, this means that a misalignment of the planet carrier leads to multi-dimensional misalignments in the form of a wobble of the planet gears. Nevertheless, in case of a planet pin position error, a displacement situation is more optimal for the most heavily loaded planet. The bearing stiffness of the sun shaft bearing determines the resulting additional loads in the overall system.
Overall System with Helical Gear Stage. After the influences of a carrier displacement in combination with a sequential mesh sequence have been shown, the results are analyzed in this section under consideration of the influence of the helical gear stage, see Figure 4. The previously applied carrier displacement is removed so that the load-related displacement of the planet carrier is applied due to the forces acting in the helical gear stage. In addition, the excitations of the helical gear stage and the interaction with the planetary gearbox are simulated.
The results of the variation of the planet pin position error are shown in Figure 11 and Figure 12. The mean values of the torque sharing factors are slightly increased compared to the statically misaligned carrier, compare Figure 9 and Figure 11. However, the range of variation increases so that the maximum torque sharing factor of the first planet increases by ΔTSFmax,flex = 0.171 for a flexible and by ΔTSFmax,stiff = 0.186 for a stiff sun shaft bearing without planet pin position error. In combination with a planet pin position error of φPPE,1 = 0.018°, the increases are larger with ΔTSFmax,flex = 0.493 for the flexible and ΔTSFmax,stiff = 0.206 for the stiff sun shaft bearing, see Figure 11 left. Overall, the highest loaded planet transmits up to 213.7% of the ideal torque due to the planet pin position error and the interaction with the helical gear stage.
This means that the excitation and the load-induced carrier misalignment of the helical gear stage has a reinforcing effect on the influence of the planet pin position error. Furthermore, the maximum and average torque sharing factors are lower with a flexible sun shaft bearing than with a stiff sun shaft bearing. The differences between the two planets 2 and 3 can be explained by the angular offset of the planets in the carrier and the excitation of specific resonance frequencies that occur only momentarily. The rotational position of the carrier at the time when the highest resonance excitation occurs thus determines the maximum effects on the individual planets.
The displacement of the sun shaft over one revolution of the carrier describes not a circle with a constant radius but with a varying radius. The mean radius of the movement increases with increasing planet pin position error and becomes larger overall in comparison to the modeling without a helical gear stage, see Figure 11. In addition, at nSun = 7,800 rpm and nSun = 9,400 rpm more significant peaks in the radial displacement are visible. The dynamic radius variation of the sun displacement, which results from the additional forces of the helical gear stage, increases up to 285% compared to the simulation with a statically misaligned carrier. Even with a planet pin position error of φPPE,1 = 0.003°, the dynamic fluctuation of the radius due to the non-ideal circular motion is significant. Overall, the dynamic fluctuation of the sun’s displacement is higher with a flexible sun shaft bearing than with a stiff one, see Figure 11 right.
The compensating movement of the sun shaft, as well as the load-induced displacement of the planet carrier lead to a higher dynamic misalignment in tooth contact. As already described in the previous section, the carrier displacement affects the first rotational order of the planet carrier in form of an oscillation of the misalignment components in the tooth contact. The forces of the helical gear stage acting on the planet carrier double these dynamic oscillations in comparison to the consideration of the only misaligned carrier, see Figure 12 left.
The average amounts of the resulting lead angle deviation are less influenced by the consideration of the helical gear stage. Here it can be seen once again that a flexible bearing of the sun shaft has no significant influence on the average displacement that occurs in the tooth contact. Rather, it reduces the compensating forces required to achieve the optimum radial sun movement for the planet affected by the planet pin position error. In turn, the lower forces required result in lower maximum pressures. The differences in the pressure in the first sun-planet mesh without planet pin position error between flexible and stiff sun shaft bearing are still small. The pressure increase with a planet pin position error of φPPE,1 = 0.018°, and a stiff bearing compared to a flexible bearing is 8.6%. If only the stiff bearing is considered, the pressure increase due to the planet pin position error of φPPE,1 = 0.018° is 18.2%, see Figure 12. Compared to the simulation with a misaligned carrier, the maximum pressure in the first sun-planet mesh is 3.7% higher with a planet pin position error of φPPE,1 = 0.018°.
When analyzing the transmission error, a lower dependence of the amplitude on the planet pin position error is visible due to the helical gear stage, see Figure 12 right. Furthermore, the excitation of the first tooth mesh order of the transmission error between sun and carrier is higher than in the simulation without helical gear stage and with the misaligned carrier. The transmission error between sun and carrier is therefore influenced by the tooth mesh orders of the following helical gear stage.
Altogether, the necessity of an integrated system modeling approach under consideration of the local misalignment conditions in the tooth contact of planetary gearboxes is clarified. The mesh sequence, the bearing stiffness of the sun shaft as well as a manufacturing-related planet pin position error have significant influences on the torque sharing and thus the increase of the tooth flank pressure and the dynamic transmission error. A comprehensive evaluation of the operational behavior of planetary gearboxes cannot be made with sufficient accuracy using simplifying methods.
Conclusion
The simulation of the operational behavior of planetary gearboxes under consideration of the load-induced interactions of the components and possible manufacturing deviations is challenging due to the dynamic displacement behavior of planetary gear stages. Within the research project “Concept ELV,2” an electrically driven rear axle for a heavy-duty distribution truck is being developed and examined with regard to its operational behavior.
The designed planetary gearbox is examined in four different model configurations with regard to the effects of a planet pin position error. First, the difference between a symmetrical and a sequential mesh sequence is considered. In the next step, a displacement of the planet carrier, which would occur in the real system due to the forces acting from the subsequent helical gear stage, is specified. Even a slight displacement of the carrier at one bearing position causes a multi-dimensional displacement of the planet gears, which thus execute a wobbling motion over one carrier revolution. This results in a higher maximum torque sharing factor as well as a higher resulting misalignment in the sun-planet mesh. This leads to higher tooth flank pressures and a higher excitation. The influence of the bearing stiffness of the sun shaft is considered. Here, as with the model configurations before, it can be seen that a more flexible sun shaft bearing has positive effects on the investigated parameters of the operational behavior.
Finally, a helical gear stage, which in the power flow follows the planetary gear stage, is also included in the simulation model. The effects of the planet pin position error are increased by the load-induced displacement caused by the forces of the helical gear stage acting on the planet carrier. Thus the maximum torque sharing factor is TSFmax = 2.137 and can be reduced to TSFmax = 1.872 with a more flexible sun shaft bearing.
The presented method offers a possibility for the quantitative evaluation of the operational behavior of integrated transmission systems. The interactions between manufacturing deviations and load-induced displacements can be simulated. In addition, the FE-based modeling of tooth contacts ensures a high quality of mesh stiffness calculation.
For further development of the method, the calculation of the local loss energy on the tooth flank and thus an efficiency analysis of an overall system under consideration of the dynamic displacement behavior is possible. In order to evaluate the load-carrying capacity, the quantitative evaluation of the tooth root stress is possible as an extension in addition to the already available pressure calculation. Furthermore, a validation of the simulation model must be performed with experimental investigations.
Acknowledgement. The authors gratefully acknowledge financial support by the Federal Ministry for Economic Affairs and Energy for the achievement of the project results.
For more Information
Questions or comments regarding this paper?
Contact Christian Westphal at c.westphal@wzl.rwthaachen.de.
References
- Klocke F.; Brecher C., 2017: Zahnrad- und Getriebetechnik. 1. Aufl, München: Carl Hanser.
- Neubauer B., 2016: Lastverteilung und Anregungsverhalten in Planetengetriebesystemen. Diss. TU München.
- Theling J.; Brecher C. et al, 2018: Einfluss von Planetenträgerabweichungen auf die lokale Lastverteilung in Planetengetrieben. In: KISSsoft AG (Hrsg) Schweizer Maschinenelemente Kolloquium, Dresden: TUDpress, S. 29–40.
- Gu X.; Velex P., 2012: A dynamic model to study the influence of planet position errors in planetary gears. Journal of Sound and Vibration 331(20): S.4554–4574.
- Papies J., 2014: Methodik zur systematischen Analyse und Optimierung dynamischer Kraft- und Weganregungen in Planetengetrieben. Diss. Ruhr-Universität Bochum.
- Iglesias M.; Fernandez del Rincon A. et al, 2017: Planetary transmission load sharing: Manufacturing errors and system configuration study. Mechanism and Machine Theory 111: S.21–38.
- Leque N.; Kahraman A., 2017: A Three-Dimensional Load Sharing Model of Planetary Gear Sets Having Manufacturing Errors. IOP Conf. Ser.: Mater. Sci. Eng. 139(3): S.2290.
- Brecher C.; Brimmers J. et al, 2019: Einfluss der dynamischen Lastverteilung in Zahnkontakten auf das Systemverhalten. In: Schlecht B. (Hrsg) Dresdner Maschinenelemente Kolloquium DMK 2019, 1. Aufl, Göttingen: sierke VERLAG - Internationaler Wissenschaftsverlag, S. 353–372.
- Cao J., 2002: Anforderungs- und fertigungsgerechte Auslegung von Stirnradverzahnungen durch Zahnkontaktanalyse mit Hilfe der FEM. Diss. RWTH Aachen University.
- Hemmelmann J. E., 2007: Simulation des lastfreien und belasteten Zahneingriffs zur Analyse der Drehübertragung von Zahnradgetrieben. Diss. RWTH Aachen University.
- Wittke W., 1994: Beanspruchungsgerechte und geräuschoptimierte Stirnradgetriebe Toleranzvorgaben und Flankenkorrekturen. Diss. RWTH Aachen University.