Design of Plastic Microgear Teeth for Mass Production with High Manufacturing Tolerances for a Medical Device
Design of Plastic Microgear Teeth for Mass Production with High Manufacturing Tolerances for a Medical Device
Jürgen Strüber
Introduction
Microgears (module < 0.2 mm) for prototype mass production have very large production tolerances in comparison with the gearwheel size. The tolerances are of the order of ±1.5% of the nominal size. Fault-free operation, i.e. — flank clearance and sufficient contact ratio — must be ensured over the entire tolerance range. A transverse contact ratio of greater than 1, which represents a conventional design rule, is no longer achievable with such large tolerances. These framework conditions set new requirements for the design and also the evaluation of microgears.
Here a tolerance-insensitive design is presented, which has a large absolute tooth depth (in mm) and a large relative tooth depth (in modules). The modifications made here ensure a smooth start to meshing over the entire tolerance range, even with a transverse contact ratio of less than 1.
Microgears have been available for decades, as, for example, in small wrist-watches. Over the last few years the range of use has grown to include other sectors such as digital cameras, model-building or medical technology. Especially in the latter sector, there is an increasing number of short-lived mass-production products which must be both inexpensive and simultaneously offer very high reliability over the specified product lifetime. Typical examples are blood glucose measuring devices and insulin pumps for diabetics: devices no bigger than a mobile phone house a mechanism that is capable of providing and evaluating measuring strips or extremely precise micropumps driven by microgear motors.
According to VDI 2731 Microgears Basic Principles (Ref. 1), the boundary between precision engineering gears and microgears is a module of 0.2 mm. With micro-gearwheels, just as for precision engineering gearwheels, the involute form is the favored tooth shape (Ref. 1). However the tolerance dimensions cannot be reduced to the same extent as the main dimensions, and thus increase relative to the component size, the smaller the gear unit becomes. Plastic injection molding is primarily used as the production process, which intrinsically has relatively wide production tolerances.
Problems and the Resulting Definition of a Task
The production-inherent tolerances of micro-gearwheels in mass production can certainly amount to 1.5% of the nominal dimension. In addition, there are large center distance tolerances due to plastic housings and long tolerance chains. The main requirements of the tolerance design are a tooth flank backlash greater than zero, and sufficient contact ratio over the entire tolerance range.
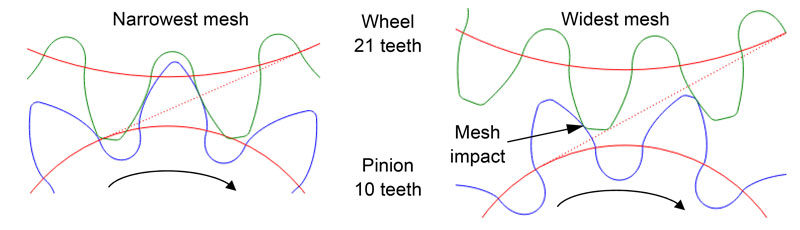
Figure 1 shows gear meshing according to a conventional design similar to DIN 58400 (Ref. 2) , with tolerances typical of a microgear. According to conventional evaluation, the transverse contact ratio must be at least 1 over the tolerance range. For the widest mesh (Fig. 1, right) there is a transverse contact ratio of less than 0.6, with a correspondingly hard impact at the start of meshing. The results are noisy running and severe wear. Consequently a gearwheel design is required that ensures operating reliability — even with large tolerances.
Design of Tolerance-Insensitive Toothing
The following requirements should be adhered to:
- Gear ratio: approx. 2
- Plastic gearwheels and housing parts can be mass-produced using a (micro-) injection molding process
- Tolerances for tip diameters, tooth thickness and center distance, as already presented
- Straight-toothed
A design insensitive to large center distance and gearwheel size tolerances requires a large absolute tooth depth in millimeters; i.e. — a trend towards a large module and a small number of teeth is necessary. With a small number of teeth, the tooth depth relative to the module is limited by undercut and by the tooth tips becoming pointed.
In contrast, the requirement for a sufficient transverse contact ratio requires a large tooth depth or a sufficiently long, involute form relative to the module which, if anything, requires a small module and large number of teeth. Below it is shown how an acceptable absolute tooth depth (in micrometers) and relative tooth depth (in modules) can be achieved. In doing so, large undercut on the pinion cannot be avoided; the mesh must be optimized by modifications.
Step 1: specification of module and number of teeth. Multiple calculations have shown that for the design optimized here, the optimum number of teeth-per-pinion is 7. Figure 3 shows a design similar to Figure 1, but with 7 teeth on the pinion.
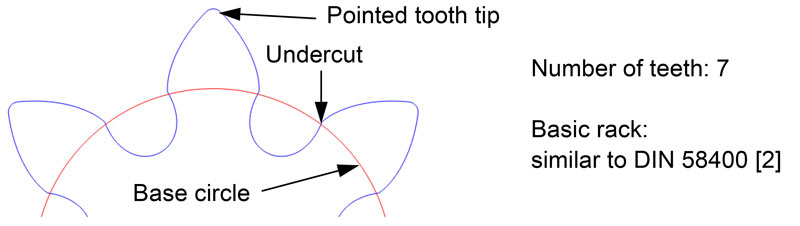
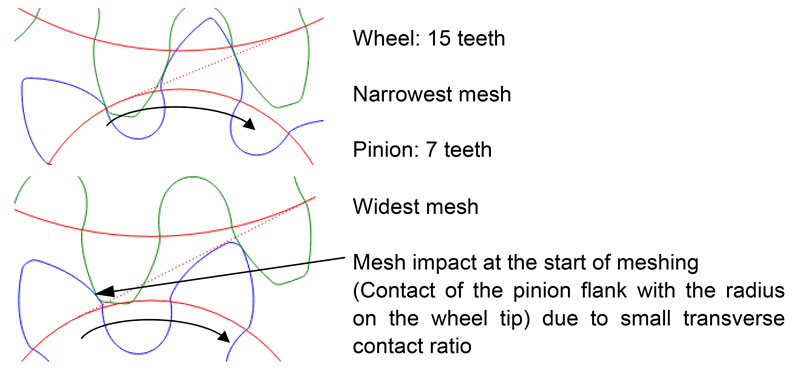
The transverse contact ratio for the widest mesh is only about 0.8. There is a mesh impact at the start of meshing. The tooth depth on the pinion cannot be further increased due to the tip limit.
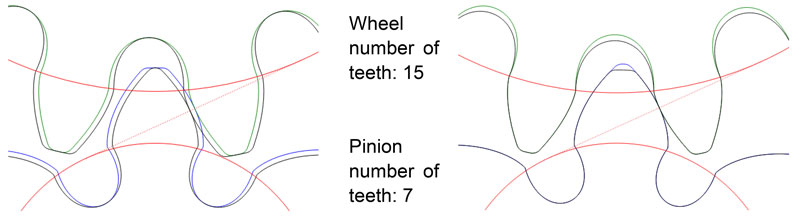
Step 2: increasing tooth depth by complementary toothing. Complementary toothing represents the state of the art: the tooth thickness of the pinion is increased while maintaining an unchanged tooth flank geometry and by counter-rotating the right and left tooth flanks about the gearwheel center. The intermeshing gearwheel is changed inversely (‘complementary’). These measures mean the teeth of the pinion are no longer pointed; therefore the tooth depth can be increased.
Step 3: increasing the tooth depth by accepting larger undercut. The tooth dedendum of the pinion and the tooth addendum of the wheel are increased; increasing of the already present undercut is accepted. Step 4: meshing optimization. At first sight the resultant meshing appears unusual, but definitely practical. Seen graphically, the contact ratio over the tolerance range is not optimal — but acceptable (Fig. 6). By calculation for the widest tolerance situation, a transverse contact ratio of approximately 0.9 results, which, while again not optimal, is a significant improvement compared with the conventional design (Table 1).
|
Table 1 Comparison: calculated transverse contact ratio for the widest mesh | ||
| Basic rack | Calculated transverse contact ratio for the widest mesh | |
| Conventional design according to Figure 1 Pinion 10 teeth, wheel 21 teeth | similar to DIN 58400 [2] | Less than 0.6 |
| Conventional design according to Figure 3 Pinion 7 teeth, wheel 15 teeth | similar to DIN 58400 [2] | approx. 0.8 |
| Increased tooth depth according to Figure 6 Pinion 7 teeth, wheel 15 teeth | special | approx. 0.9 |
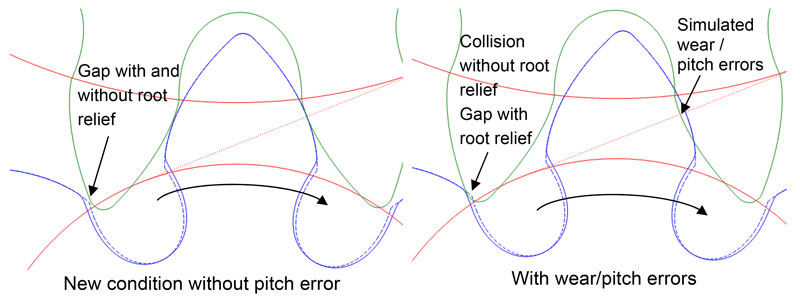
The mesh as shown in Figure 6 still exhibits weak points; if tooth flank wear and pitch errors are considered, then, particularly with narrow meshing, the result may be a hard mesh impact or premature contact.
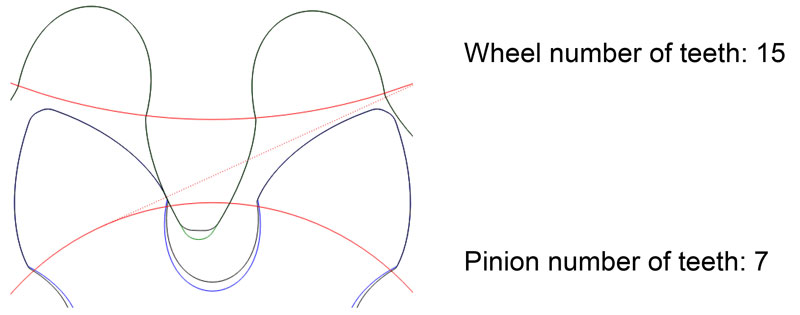
To prevent this collision the pinion is given root relief that, in comparison with more usual root relief, primarily recesses the dedendum in the area of the root surface or the undercut, and mandatorily only removes a small element from the involute form.
Figure 7 clarifies how this measure prevents a collision before the desired meshing. However, a small part of the involute form is lost, which further reduces the calculated transverse contact ratio for the widest mesh. It is for this reason that it is explained in the following which design and mesh are to be favored.
Evaluation and Advantages of the Optimized Design
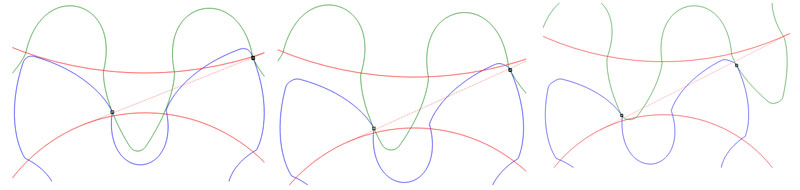
With the optimized design, meshing takes place smoothly and close to the pitch point. Very similar meshing conditions exist over the entire tolerance range; the pinion involute is shorter than that of the wheel. The whole involute of the pinion engages throughout the entire tolerance range with the wheel flank. The involute used by the wheel lies more in the outer, middle or inner area of the involute, dependent on the tolerance situation. The start of meshing takes place over the entire tolerance range below the wheel tooth tip, which ensures a smooth meshing start.
Figure 8 shows that in the optimized design the flank gap decreases in slower fashion and the contact starts later (that is, closer to the pitch point) than with the conventional design. Moreover, with the conventional design there is a meshing impact for the widest mesh because of the overly small transverse contact ratio. With the optimized design the meshing start is smooth, even for the widest mesh, with a transverse contact ratio significantly less than 1. At the conventional design pitch, error and wear can significantly amplify the mesh impact, while with the optimized design the start of meshing is indeed moved, but remains ‘smooth’ nevertheless.
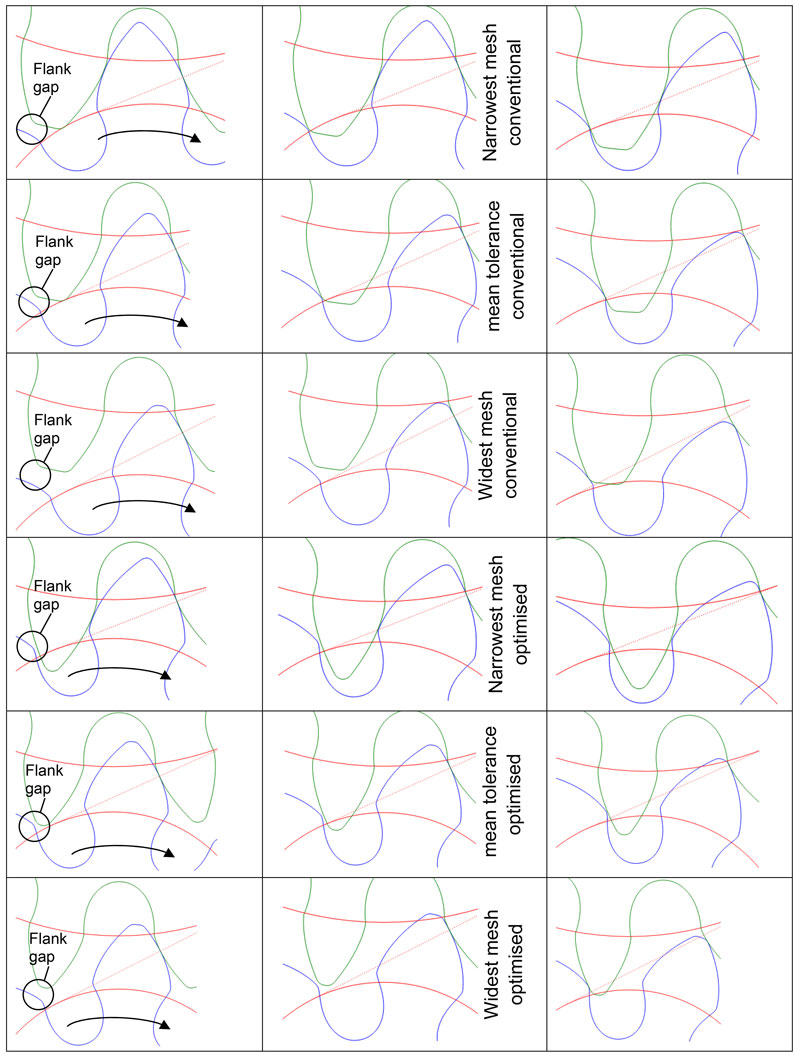
Figure 9 shows the calculated geometric transmission error for the conventional and optimized design — without elastic deformation and without pitch errors. The wide plateaus represent areas in which the involutes are in contact. The downward peaks are those areas between the involute engagements. Therefore the width of the peaks is a measure of how much the transverse contact ratio is less than 1. Indeed, the transmission error (more accurately, the difference between maximum and minimum values subsequently referred to as Δ transmission error) for the narrowest and medium mesh for the conventional design is approximately zero; by contrast, the widest tolerance situation is equal to a difference of about 4 µm. For the optimized design there are similar curves for the transmission error for the three tolerance situations. The difference between maximum and minimum value is between 2.0 and 2.7 µm, dependent on the tolerance situation. Moreover, the downward peak for the conventional design for the widest mesh is narrower than for the optimized design.
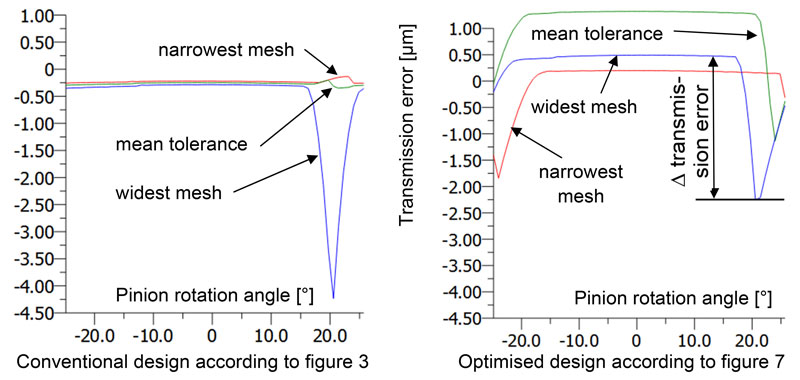
Metaphorically speaking, the transmission error represents for the conventional design a ‘narrow, deep pothole,’ while for the optimized design it represents a ‘wide, flat depression.’
Although a transverse contact ratio greater than 1 over the entire tolerance range is desirable, it is, however, not possible with large tolerances relative to the component size. Also, solely maximizing the transverse contact ratio is not appropriate. Table 2 very clearly indicates for the widest mesh that a smaller transverse contact ratio can even have a smaller transmission error as a consequence.
|
Table 2 Comparison: computed transverse contact ratio and Δ transmission error | |||
| Conventional (Figure 3) | Optimized (Figure 7) | ||
| Narrowest mesh | Transverse contact ratio | 1.0 | 0.77 |
| Δ transmission error [µm] | 0 | 2.0 | |
| Mean tolerance | Transverse contact ratio | 0.95 | 0.74 |
| Δ transmission error [µm] | ˜ 0 | 2.3 | |
| Widest mesh | Transverse contact ratio | 0.80 | 0.71 |
| Δ transmission error [µm] | 4.0 | 2.7 | |
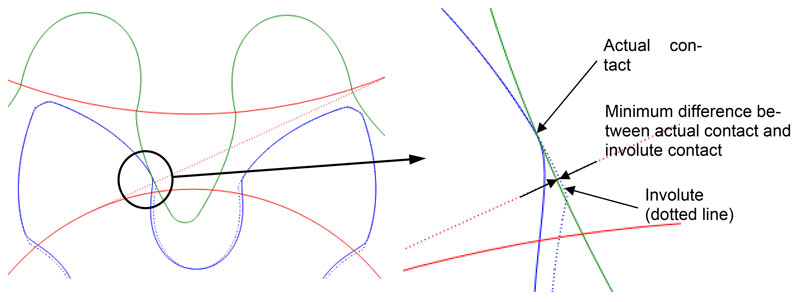
One reason the value of the computed transverse contact ratio for such toothing systems is to be considered with caution is that, as a result of undercut or root relief, there is from a calculated viewpoint no contact in the area of the involute. The difference between the actual contact and the involute contact may, however, be in the sub-micrometer range, i.e. — negligible in practice.
For evaluation of corresponding optimized toothing systems, it is therefore suggested that less consideration be given to the transverse contact ratio and that most attention be paid to transmission error. Moreover, the mesh, especially the start of the mesh, should be visually considered, which in fact partially results in a somewhat subjective assessment.
Outlook
A design for microgears was presented that ensures uniform operation over a wide tolerance range. Corresponding gears were constructed and found to function well during internal tests and customer trials. Viewed under the microscope, the parts look like ‘actual gearwheels’ with tooth flank contours that correspond to the figures shown. However when the gearwheels are viewed with the naked eye, the question nevertheless arises — to what extent optimizations in the micrometer range on plastic parts remain solely of an academic nature, and whether (to put it bluntly) triangular teeth with rounded tip and root would not also serve the same purpose. Experience has shown that small, plastic gearwheels are in practice much more tolerant to deviations than would be expected from pure theory.
In the sense of a proof of reliability for demanding medical devices, the theoretical considerations are nevertheless not at all in vain. There are very few standards dealing with microgears; VDI 2731 (Ref. 1) cited at the beginning refers not for nothing to Microgears: Basic Principles. Here the state of the art and the differences relative to larger gears in respect to design, production or measuring technology are presented. ‘It is intended to provide a basic repository of information, to stimulate discussion, and, in the longer term, expansion,’ as explained in S ection 1 of VDI 2731 (Ref . 1). However, etched-in-stone design guidelines for, example, basic racks or tolerance values, are not included.
Miniaturization is just beginning.
References
- VDI 2731, Part 1. Microgears: Basic Principles, Beuth Verlag GmbH, Berlin, April 2009.
- DIN 58400 (withdrawn without replacement). Basic Rack for Involute Teeth of Cylindrical Gears for Fine Mechanics, Beuth Verlag GmbH, Berlin, June 1984.